Dichtung und Wahrheit hinter Heisenbergs Quantenrevolution
Ein befremdliches mathematisches Konzept verhalf der Quantenphysik vor 100 Jahren zum Durchbruch. Nun ließ sich die Welt der Atome berechnen. Doch wie soll man sie verstehen? Kann man das überhaupt? Bald gab es konkurrierende Ansätze, und die Deutungen sind bis heute umstritten.
Wer die Revolution der Quantenmechanik begreifen will, begegnet zwei verschiedenen Geschichten. Die erste ist eine Heldenstory. Folgt man ihr, gelangt man zu einem ganz bestimmten Punkt in Raum und Zeit – mit einem entscheidenden Geistesblitz, der das Verständnis der subatomaren Welt umwälzen sollte.
Die Heldengeschichte geht so: Die physikalische Welt erschüttern zu Beginn des 20. Jahrhunderts unerklärliche Messungen an Licht und Atomen. Bei den Deutungsversuchen verstrickt sich die Fachgemeinschaft über Jahre in Widersprüche; die Physiker, die sich bis dahin im Zenit der Erkenntnis wähnten, können die seltsamen Phänomene nicht stimmig erklären. Die bewährten Vorstellungen und klassischen Bilder versagen. Die Physik befindet sich in einer Krise.
Auftritt Werner Heisenberg. Im
Frühsommer des Jahres 1925 hat der gerade einmal 23-jährige
Physikstudent aus Göttingen die Nase voll. Nicht nur im übertragenen
Sinn. Ihn plagt zwar einerseits die verfahrene theoretische Lage. Vor
allem aber lässt ihn lähmender Heuschnupfen keinen klaren Gedanken
fassen. Beides will er mit einem Urlaub auf der deutschen Hochseeinsel
Helgoland ändern. Und tatsächlich: Fernab sowohl von den Pollen als auch
den Ablenkungen des Festlands klart sich Heisenbergs Geist auf. Das
junge Genie blickt auf völlig neue Weise auf das größte Rätsel der
damaligen Physik.
Die Quantenmechanik war von Anfang an heftig umstritten. Auch 100 Jahre später ist sich die Fachwelt nicht einig: Was verraten die Formeln über die Realität? In dieser Themenwoche hinterfragen wir, was nötig ist, um die wahre Natur der Teilchen zu begreifen. Womöglich braucht es eine völlig andere Herangehensweise.
100 Jahre Quantenmechanik: Dichtung und Wahrheit hinter Heisenbergs Quantenrevolution
Realität: Warum selbst Physiker die Quantenmechanik nicht verstehen
Quanten-Holonomie-Theorie: Eine neue Verbindung von Raum, Zeit und Quantenphysik
Kommentar: Quantenphysik hat nichts mit Esoterik zu tun
Springers Einwürfe: Die Zukunft der Quanten
Nobelpreisträger 't Hooft: »Der Grund, warum es nichts Neues gibt, ist, dass alle gleich denken«
Zurück in Göttingen bringt er seinen konzeptionellen Durchbruch zu Papier und reicht ihn Ende Juli 1925 zur Veröffentlichung ein. Bereits das Wort »Umdeutung« im Titel der Publikation macht klar, wofür Heisenberg hier plädiert: eine radikal andere Sicht auf klassische Konzepte.
Es
führe in die Irre, argumentiert Heisenberg, das befremdliche Verhalten
der unsichtbaren Partikel anschaulich beschreiben zu wollen. Deswegen
mussten alle scheitern, die das bisher versucht hatten. Stattdessen
dürfe man lediglich die nüchternen Messergebnisse heranziehen, so
verwirrend die einzelnen Beobachtungen auch sein mögen. Es brauche einen
neuen mathematischen Formalismus. Der liefere dann ein
widerspruchsfreies Modell vom Reich der kleinsten Teilchen, unbelastet
von herkömmlichen Vorstellungen.
Entsprechende
Rechenvorschriften skizziert Heisenberg in seinem Artikel. Auf diesen
lässt sich endlich eine funktionierende, allumfassende Quantentheorie
aufbauen – und mit ihr die Atomphysik von Grund auf neu errichten.
So
weit die erste Erzählung. Die zweite ist verwobener, vielschichtiger.
Sie spielt nicht auf den zerklüfteten Felsen der kargen Hochseeinsel,
sondern zwischen sanften, bewaldeten Hügeln in Göttingen. In der
preußischen Universitätsstadt kommen seit einigen Jahren die größten
mathematischen und naturwissenschaftlichen Genies zusammen. Sie ist nur
eine Tagesreise entfernt von weiteren Hotspots der europäischen Physik
wie Kopenhagen und München. Überall diskutieren die klügsten Köpfe des
frühen 20. Jahrhunderts über die neuen Erkenntnisse und deren Deutungen,
besuchen sich, tauschen Briefe aus. Ansätze aus den verschiedenen
Fachgebieten und unterschiedliche Ansichten befruchten sich gegenseitig.
Letztlich entscheidet Kooperation statt Isolation. Nur dem Schmelztiegel heiß diskutierter, oft gegensätzlicher, unkonventioneller Ideen kann eine Theorie entspringen, die anders ist als alles, was man bisher kannte: eine Weltsicht, konzeptionell so anspruchsvoll und mathematisch so befremdlich, dass es die Leistungsfähigkeit selbst des größten Geistes überstiege, sie einsam in einem kreativen Rausch zu erdenken.
Innerhalb
weniger Jahre entstehen verschiedene Formelwerke und philosophische
Interpretationen der neu begründeten Quantenmechanik. Es entbrennt ein
leidenschaftlich geführter Streit darüber, welche Perspektive die wahre
Natur der Teilchen am besten erfasst. Zu keinem Zeitpunkt war auf einen
Schlag alles klar. Im Gegenteil dauert zu manchen Fragen die Debatte bis
heute an.
Beide
Erzählungen scheinen nicht zusammenzupassen. Aber wer sich mit
Quantenmechanik beschäftigt, muss sich an Irritationen gewöhnen.
Wer sich mit Quantenmechanik beschäftigt, muss sich an Irritationen gewöhnen
Zum widersprüchlichen Wesen der Quanten gehört es, dass mitunter grundverschiedene Dinge nebeneinander existieren. Etwas kann sowohl grenzenlos ausgedehnte Welle als auch kompaktes Teilchen sein. Objekte befinden sich irgendwie an einem Ort und zugleich an einem anderen. Lässt sich so etwas überhaupt verstehen, und welche entscheidenden Konzepte braucht es dafür? Der Geschichte der Quantenmechanik nachzugehen hilft dabei, ihre zentralen Ideen zu begreifen und zu etwas vorzudringen, was zum Fundament der modernen Physik wurde.
Die Welt in Feierlaune
Jeder
liebt gute Heldengeschichten, auch die physikalische Community. Deshalb
haben die Vereinten Nationen das Jahr 2025 – genau 100 Jahre nach dem
Erscheinen von Heisenbergs Umdeutungs-Paper – zum »Internationalen Jahr
der Quantenwissenschaften und Quantentechnologien« ausgerufen.
Um
bloß keine Missverständnisse aufkommen zu lassen, auf welche Geschichte
sich die Organisatoren bei dem Jubiläum beziehen, veranstalteten sie
eine hochrangig besetzte wissenschaftliche Konferenz auf Helgoland.
Spitzenforscher, darunter mehrere Nobelpreisträger, trafen sich Anfang
Juni 2025 zu einem mehrtägigen Workshop auf der Insel.
Dort besprachen sie die größten Herausforderungen der modernen
Quantenphysik: Quanteninformatik, mögliche Wege zu einer
Quantengravitation, die Grenzen zwischen klassischer und Quantenwelt.
Auf
einem Wanderweg konnten die Teilnehmenden an einem Gedenkstein
vorbeigehen, der seit einem Vierteljahrhundert dem rauen Klima
Helgolands trotzt. Auf der Plakette steht: »Im Juni des Jahres 1925
gelang hier auf Helgoland dem 23-jährigen Werner Heisenberg der
Durchbruch in der Formulierung der Quantenmechanik, der grundlegenden
Theorie der Naturgesetze im atomaren Bereich, die das menschliche Denken
weit über die Physik hinaus tiefgreifend beeinflusst hat.« So erzählte
man es sich im Juni 2000, als die Deutsche Physikalische Gesellschaft
die Tafel gemeinsam mit dem Max-Planck-Institut für Physik in München
enthüllte, das Werner Heisenberg bis zu seiner Emeritierung Ende 1970
leitete. 
Gedenkstein für Werner Heisenberg auf Helgoland | Seit dem Jahr 2000
steht auf Helgoland ein Stein, der an Heisenbergs »Durchbruch in der
Formulierung der Quantenmechanik« auf der Insel erinnert.
Streit ums Allerkleinste
Den dramaturgischen Rahmen für die Heldengeschichte der Quantenmechanik setzt eine ebenso beliebte Erzählung: Im ausklingenden 19. Jahrhundert sei noch kein Hauch von Revolution zu spüren gewesen. Im Gegenteil hätten die zeitgenössischen Physiker selbstgefällig auf das eigene Fachgebiet geblickt. Mit den bis dahin gefundenen Gesetzen – der Mechanik, dem Elektromagnetismus und der Thermodynamik – schienen sich alle Vorgänge begreifen zu lassen, bis hinab zum gerade erst entdeckten Reich der Atome. So schien es dem Experimentalphysiker und späteren Nobelpreisträger Albert Michelson im Jahr 1894 »wahrscheinlich, dass die meisten der grundlegenden Prinzipien bekannt sind«. Die Zukunft der Physik läge in Präzisionsmessungen.
Doch auch dahinter steckt eine etwas kompliziertere Wahrheit. Schon zur Jahrhundertwende wurde deutlich, dass mit den bekannten Regeln der Physik etwas nicht stimmen konnte. Das offenbarten nicht etwa exotische Phänomene, sondern ganz banale, vorderhand klassische Zusammenhänge. Es ging um die scheinbar einfache Frage, welche Strahlung ein heißer Körper abgibt.
Wer
ein Stück Metall erhitzt, sieht es erst rötlich schimmern. Mit höherer
Temperatur kommen weitere Farben hinzu, und das Werkstück glüht orange,
gelb, schließlich grellweiß. Das Ganze – in idealisierter Form – zu
beschreiben, klappte mit den etablierten Formeln aber nicht. Es kam zur
»Ultraviolettkatastrophe«: Bei immer kürzeren Wellenlängen, das heißt in
Richtung des ultravioletten Bereichs, schien die Energie der
abgegebenen Strahlung unendlich groß zu werden. Unendlichkeiten ergeben
in der Physik keinen Sinn, hier stimmte etwas nicht.
Im
Jahr 1900 fand der deutsche Physiker Max Planck eine Formel, mit der er
die Ultraviolettkatastrophe abwenden konnte. Doch dafür musste Planck
annehmen, dass Atome die Strahlung nur in Form kleinstmöglicher
Energiehäppchen abgeben. Heute würden wir sagen: in Quanten. Das war zu
diesem Zeitpunkt überhaupt nicht einleuchtend, sondern erstmal bloß ein
mathematisches Experiment. Planck hatte zur Berechnung der
Mindestenergie rein behelfsmäßig eine Konstante h eingeführt. Das funktionierte. Entgegen seiner Erwartungen gelang es Planck aber anschließend nicht, sein h wieder aus den Formeln zu beseitigen.
Die
Konstante ließ Planck nicht mehr los, bis in den Tod. Seinen schlichten
Grabstein auf dem Stadtfriedhof Göttingen zieren nur zwei Dinge. Ganz
oben sein Name, schnörkellos. Dicht über dem Boden, inmitten floraler
Verzierungen, h und ihr Wert. Auf dieser Basis erwuchs eine neue Physik.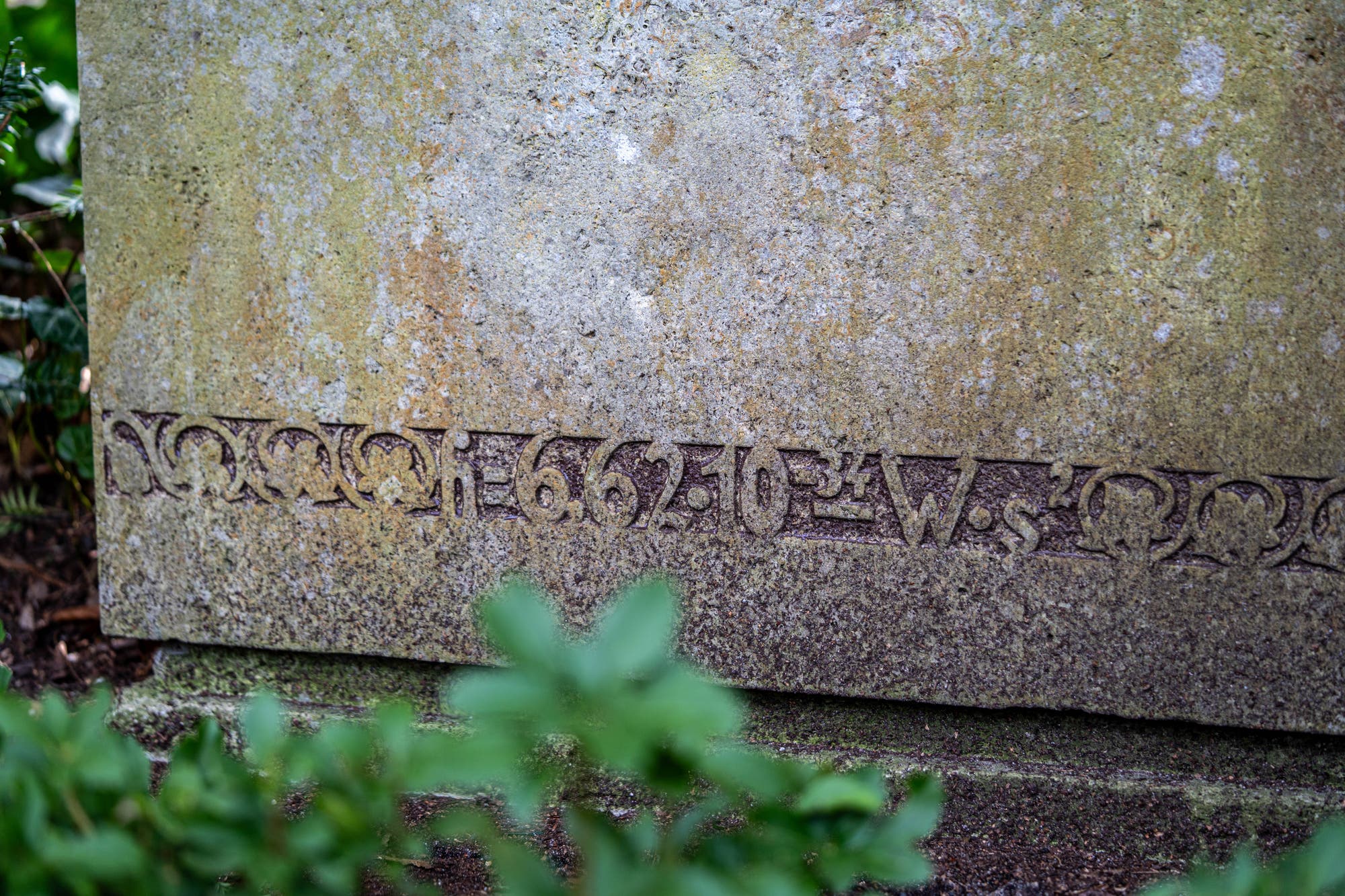 
Grundlegende Konstante | Die von Max Planck eingeführte Konstante h liegt am Fundament der Quantenmechanik. Außerdem ist der Wert von h = 6,62 · 10-34 W · s2 am Fuß des Grabsteins des Physikers eingraviert.
Mit Plancks Konstante waren die Quanten gekommen, um zu bleiben. E = hν, die Energie von Strahlung entspricht Portionen von h mal ihrer Frequenz, diese einfache Gleichung war Ausdruck etwas grundlegend Neuem.
Und
so feierten viele Institutionen, etwa die Deutsche Physikalische
Gesellschaft, das 100. Jubiläum der Quantenphysik bereits im Jahr 2000.
Weitere Anlässe folgten bald.
Ausgerechnet Albert Einstein, der vorrangig für seine kosmologischen Errungenschaften und für seine spätere kritische Haltung gegenüber der Quantenmechanik bekannt ist, brachte im Jahr 1905 die Quanten in die Atomphysik. Er erklärte den mysteriösen »photoelektrischen Effekt«, der zuvor im Labor gemessen worden war. Hierbei schlägt Strahlung Ladungsträger aus der Oberfläche eines Materials heraus – allerdings nicht, wie erwartet, abhängig von der Intensität des Lichts, sondern von dessen Frequenz. Um das zu erklären, schrieb Einstein dem Licht, das seit einem Jahrhundert gesichert als Welle galt, den Charakter eines Teilchens zu. Es überträgt seine Energie nicht kontinuierlich, sondern in Form kleiner Pakete, als Lichtquanten. Diese Erkenntnis brachte ihm später den Nobelpreis ein – und nicht seine Relativitätstheorien.
Im Jahr 1913 ging es auch
dem Dänen Niels Bohr um seltsame Versuchsergebnisse. Der experimentelle
Befund: Die negativen Ladungsträger kleben nicht im restlichen Atom wie
in einem Rosinenbrötchen. Vielmehr konzentriert sich die positive Ladung
auf einen Kern, und die Elektronen bewegen sich offenbar irgendwie
drumherum. Doch den klassischen Gesetzen zufolge müssten sie während
ihrer Drehung Energie abgeben und deshalb innerhalb kürzester Zeit in
den Kern stürzen. Aber Atome verlieren keine Energie, sondern sind
stabil. Mit einem neuen Atommodell gelang Bohr eine Erklärung. Demnach
kreisen Elektronen verlustfrei auf ganz bestimmten Bahnen um den
Atomkern. Der Bereich dazwischen ist ihnen verboten: Von Bahn zu Bahn
kommen sie nur, indem sie Energie in exakt passenden Portionen aufnehmen
oder abgeben – durch einen Quantensprung. Auch dieses Bild war
wegweisend, und auch Bohr erhielt dafür einen Nobelpreis.
Bohrsches Atommodell
Als
sich zu Beginn des 20. Jahrhunderts herausstellte, dass sich die
positive Ladung eines Atoms auf einen kompakten Kern konzentriert,
geriet die klassische Anschauung an ihre Grenzen. Denn dann müssten sich
die negativ geladenen Elektronen in der Atomhülle um den Kern bewegen
wie Planeten um die Sonne. Doch nach den Regeln der Elektrodynamik
strahlt eine kreisende Ladung elektromagnetische Wellen ab. Damit sollte
das Elektron Energie verlieren und müsste innerhalb kürzester Zeit in
den Kern stürzen.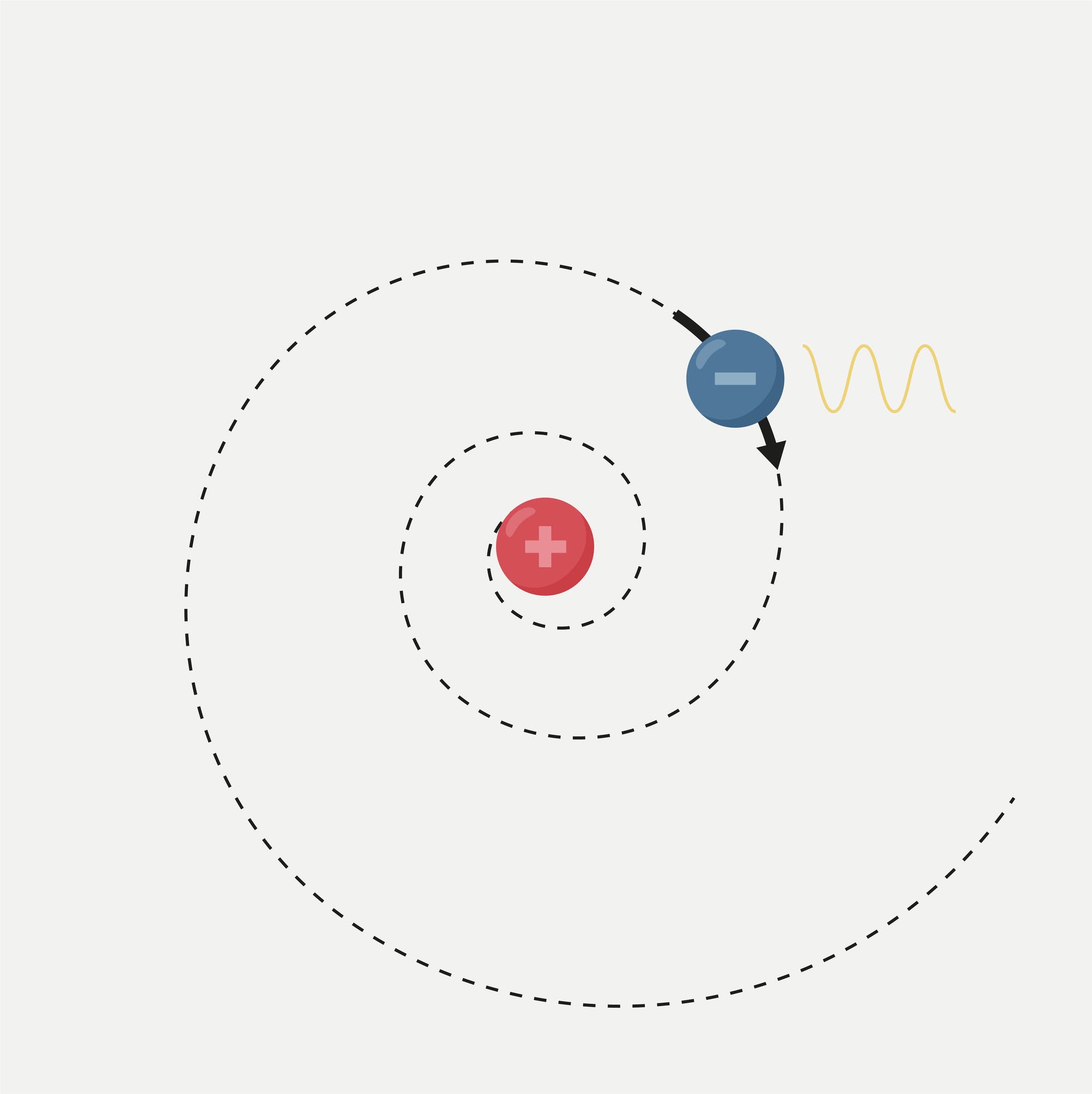 
Mit
seinem im Jahr 1913 entwickelten Modell löste Niels Bohr das Problem.
Bohr postulierte bestimmte Bahnen, auf denen Elektronen sich befinden
können, ohne Energie zu verlieren. In den dazwischen gelegenen Bereichen
halten sich die Teilchen nicht auf. Sie können allerdings von einer
Bahn zur anderen wechseln, indem sie Strahlung einer genau definierten
Wellenlänge aufnehmen oder abgeben.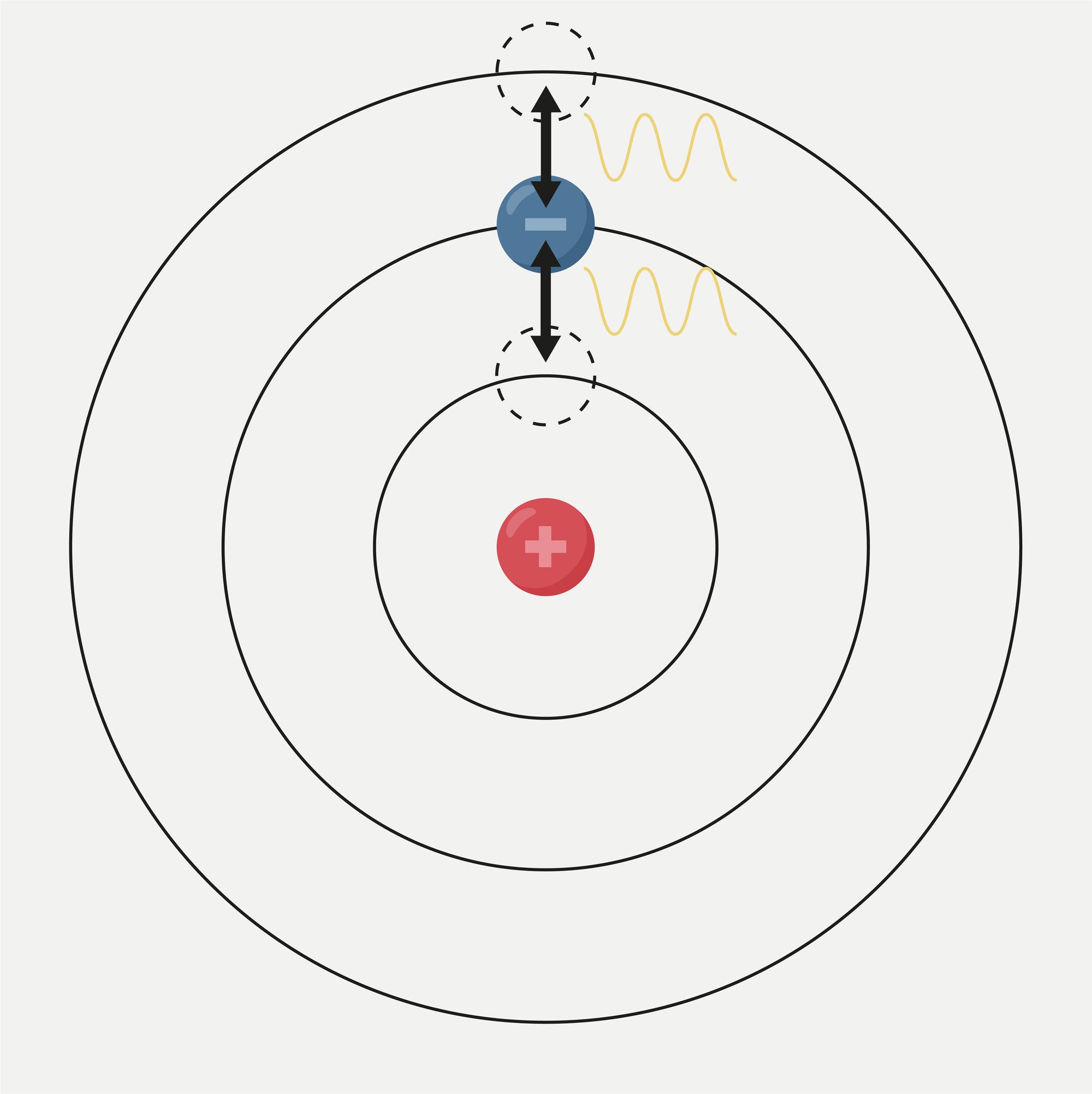 
Dieses
Modell konnte einige experimentelle Resultate erklären, insbesondere
die spektralen Übergänge beim Wasserstoff und die diskreten
»Quantensprünge« bei den Energien. Es bot ein anschauliches Bild für die
einfachsten Vorgänge im Atom, versagte aber bei komplizierteren
Phänomenen.
Das sind zwei Beispiele für diverse Ideen zwischen den Jahren 1900 und 1925, die mit herkömmlichen Ansichten brachen, die Quantenphysik voranbrachten und sogar Nobelpreise wert waren. Was also macht Heisenbergs Beitrag so besonders?
Alle Konzepte krankten an einem Problem: Sie bedienten sich an Bildern aus der klassischen Erfahrungswelt
Bis zum Jahr 1925 gab es viele Modelle zu einzelnen Phänomenen, aber es fehlte eine konsistente mathematische Beschreibung. Denn alle Konzepte krankten an einem Problem: Sie bedienten sich an Bildern aus der klassischen Erfahrungswelt, um die Vorgänge irgendwie begreiflich zu machen. Für Heisenberg war das der zentrale Fehler. Schließlich hatte niemals jemand ein Elektron auf einer Bahn um einen Atomkern kreisen sehen. Heisenberg ließ nur zwei Dinge gelten: Beobachtungsgrößen, die sich unzweifelhaft messen lassen, und mathematische Operationen, um sie miteinander zu verbinden.
Die große Revolution der
Quantenmechanik gelang nicht wegen neu entwickelter Vorstellungen davon,
was mit Atomen und Strahlung passiert. Vielmehr war es nötig, sich von
solchen Bildern zunächst komplett zu lösen.
Heisenbergs große Umdeutung
Zu
dem, was auf Helgoland passiert ist, hat Heisenberg selbst Jahrzehnte
später seine Version aufgeschrieben. Sie ist der Ursprung der oft
erzählten Heldengeschichte. »Durch eine nach heutigen Maßstäben
reichlich umständliche Rechnung«, resümierte Heisenberg im Jahr 1969 in
seiner Autobiografie »Der Teil und das Ganze«, habe er in einer Tabelle
die einzelnen Terme zu den Beobachtungsgrößen bestimmt. So bewies er
seinen eigenen Worten zufolge die »mathematische Widerspruchsfreiheit
und Geschlossenheit der damit angedeuteten Quantenmechanik«.
Rückblickend beschrieb er, wie er in einer Art Erweckungserlebnis »durch die Oberfläche der atomaren Erscheinungen hindurch auf einen tief darunter liegenden Grund von merkwürdiger Schönheit« schaute. Heute überwiegen in der Geschichtsforschung Zweifel daran, dass Heisenberg wirklich einen solchen Heureka-Moment hatte. Die geradezu naturromantische Story von einer plötzlichen Erleuchtung entspringt Heisenbergs eigener, verklärender Dramatisierung einige Jahrzehnte später. Zeitgenössische Quellen machen klar, dass Heisenberg zunächst an der Tragweite seiner Ideen zweifelte und sich bei Kollegen rückversicherte, dass er überhaupt auf der richtigen Spur war.
Jedenfalls, so viel ist sicher, reichte Heisenberg seine Erkenntnisse am 29. Juli 1925 bei der »Zeitschrift für Physik« zur Veröffentlichung ein.
Heisenbergs Umdeutung
Von klassischer Physik zur Quantentheorie
Allerdings besaß Heisenbergs Schema aus damaliger Sicht eine Schwäche. Gerade die sollte sich aber als wegweisend für die neue Quantenmechanik herausstellen: Die Berechnungen waren nichtkommutativ. Demnach würde die Reihenfolge, mit der man physikalische Größen misst, den Ausgang eines Experiments beeinflussen. Ob man erst die Geschwindigkeit eines Teilchens anschaut und dann seinen Ort, liefert andere Ergebnisse, als wenn man den Ort zuerst feststellt und dann die Geschwindigkeit. Beide Messungen lassen sich nicht folgenlos vertauschen.
Vor allem aber waren Heisenbergs
Berechnungen nicht sonderlich elegant. Als er sie in Göttingen
selbstkritisch seinem Institutsleiter Max Born vorlegte, erkannte
dieser: bestimmte mathematische Objekte könnten das Ganze erheblich
vereinfachen, nämlich Matrizen, eine Art Tabelle. Bis zu diesem
Zeitpunkt waren Matrizen mit ihren eigenwilligen Regeln – auch
Matrizenrechnung ist nicht kommutativ – in der Physik nur vereinzelt
genutzt worden. Sie galten als abstrakte Objekte der reinen Mathematik.
Born war selbst nicht besonders geübt auf dem Gebiet. Sein ehemaliger
Student Pascual Jordan kannte sich da besser aus. Jordan hatte in
Göttingen dem Mathematiker Richard Courant bei dessen Arbeit am
zukünftigen Lehrbuchklassiker »Methoden der mathematischen Physik«
assistiert. Ein zentrales Thema: Matrizen.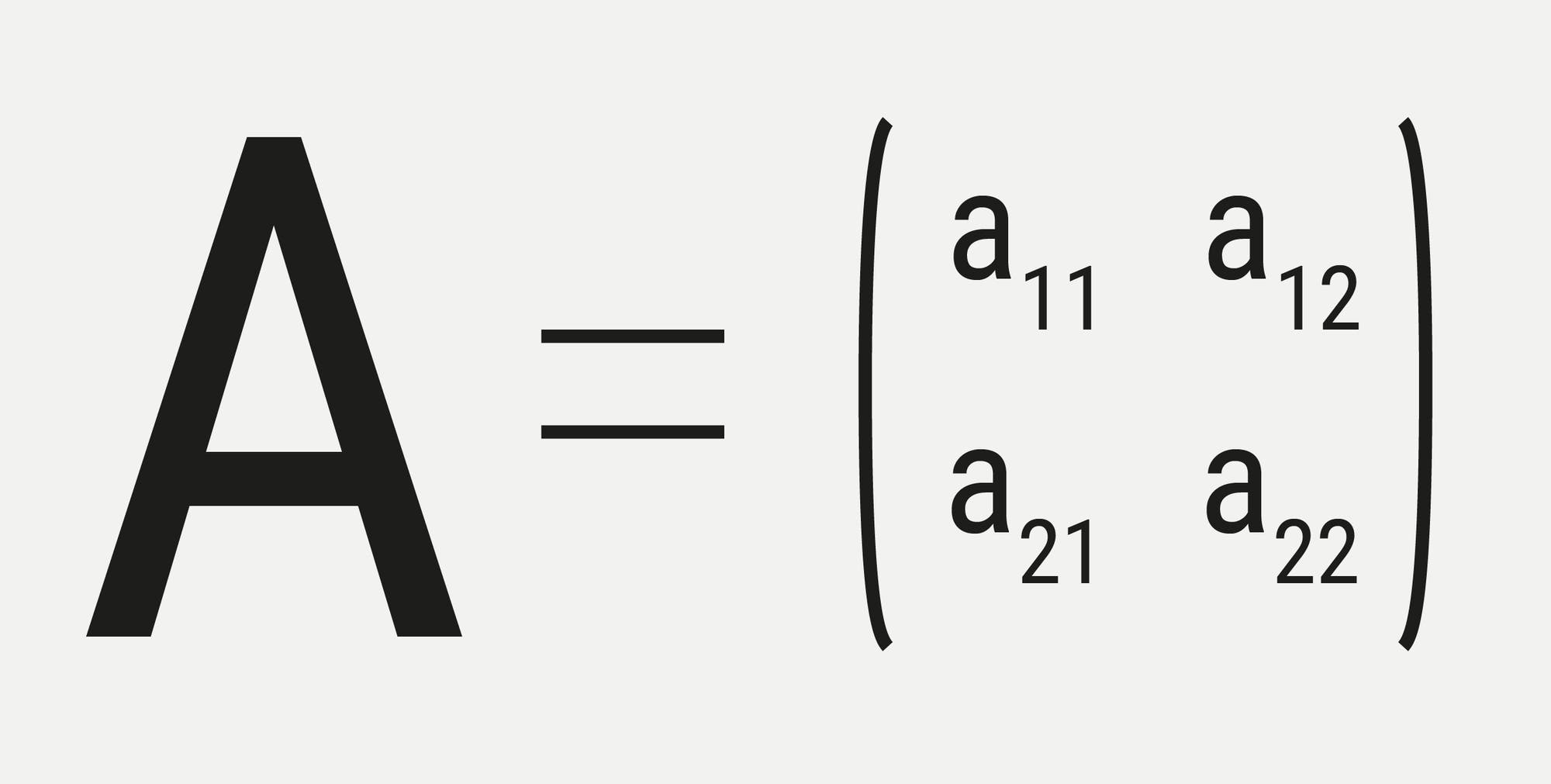
Eine
Matrix ordnet verschiedene Elemente in einer Tabelle an. Bei diesem
einfachen Beispiel besteht sie aus vier mathematischen Objekten in je
zwei Zeilen und Spalten. Matrizen können aber auch sehr viel mehr
Elemente enthalten, und sie müssen nicht quadratisch sein: Jede
Kombination von Zeilen- und Spaltenzahl ist möglich.
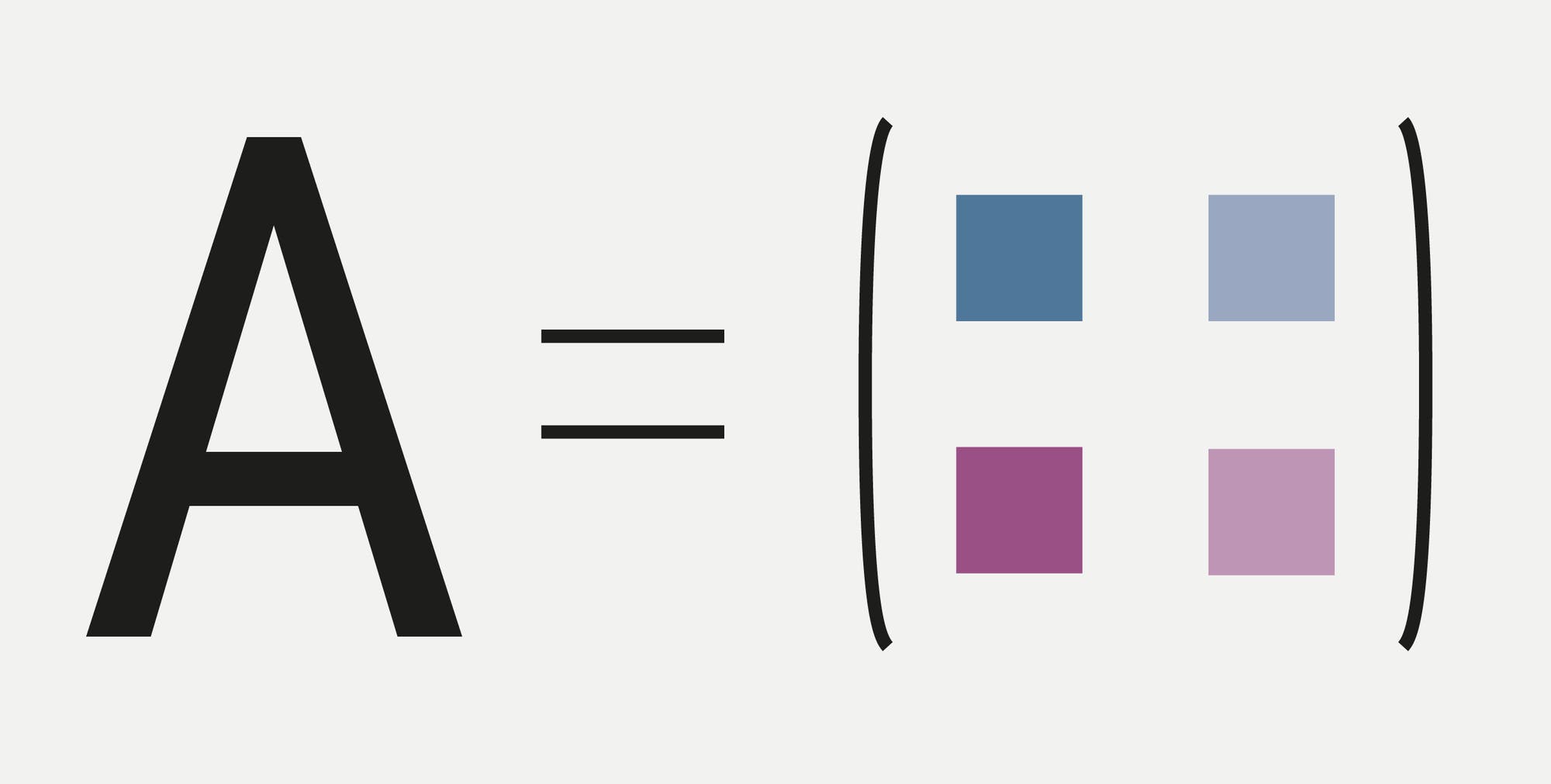Die Objekte in einer Matrix können vielfältig sein. Hier sind es vier Farben.
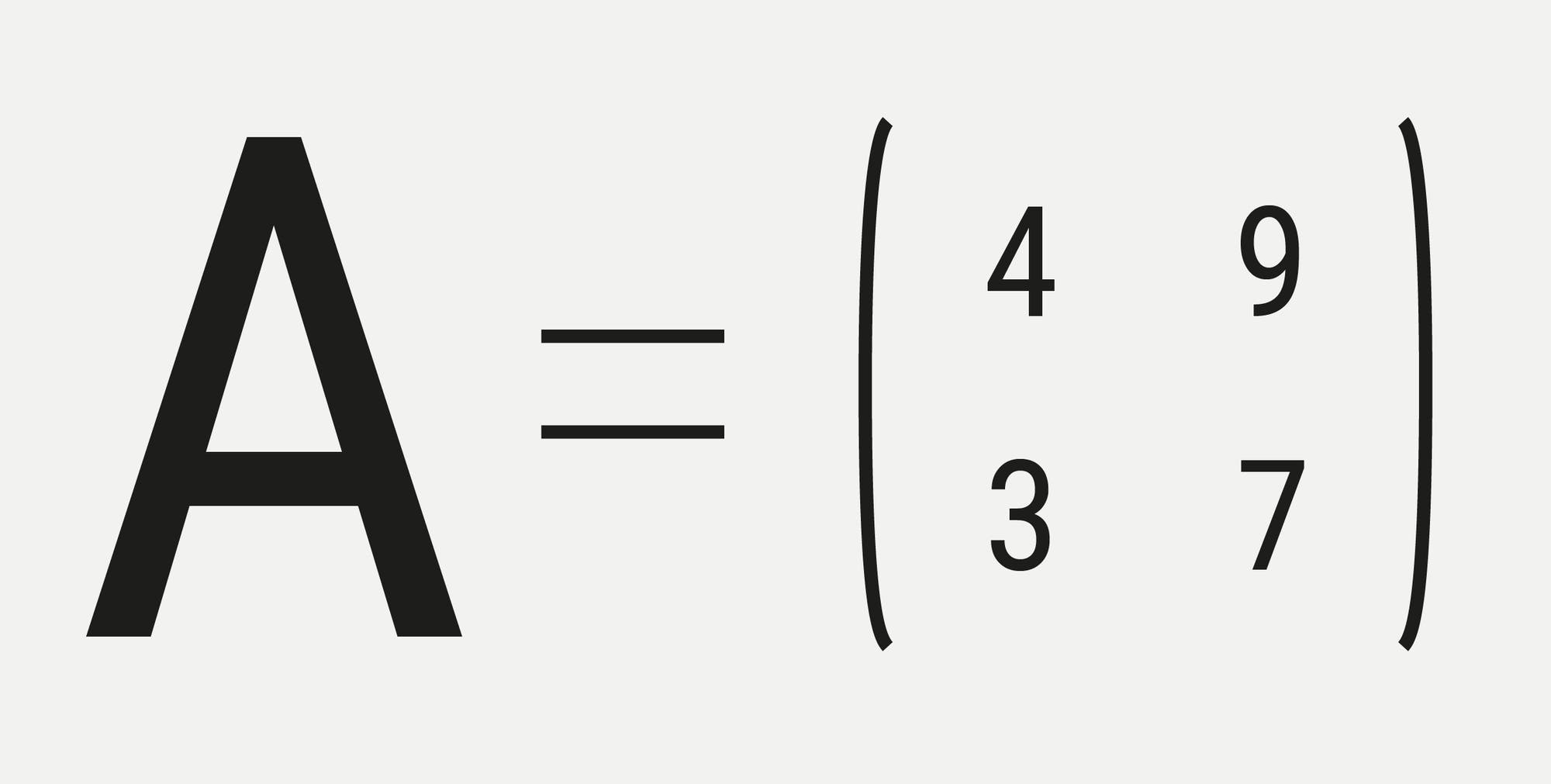Oft enthalten Matrizen einfach Zahlenwerte. In der Physik lassen sich
damit zum Beispiel Bewegungen, Drehungen und andere Prozesse im Raum
beschreiben. Eine 2x2-Matrix würde man für den zweidimensionalen Raum
nutzen, eine 3x3-Matrix für drei Raumdimensionen, und in der
Relativitätstheorie sind vier Zeilen und Spalten üblich, um zusätzlich
die Zeitdimension zu betrachten.
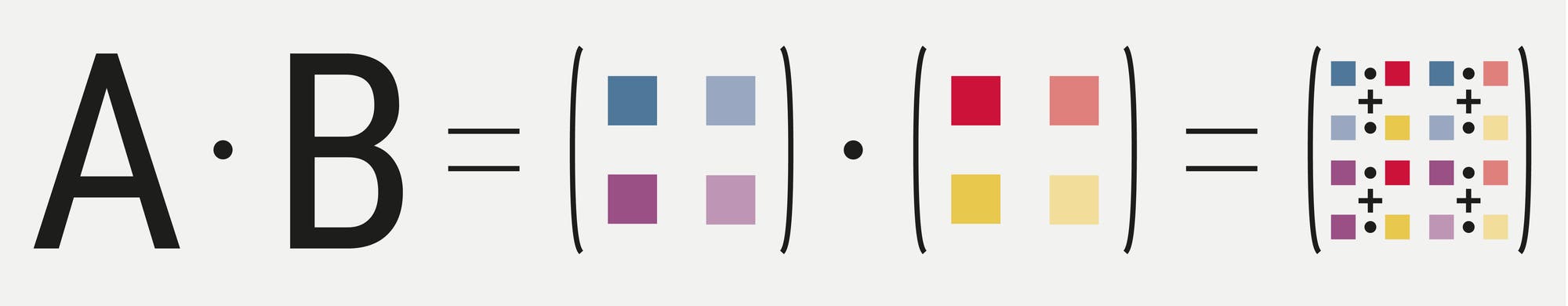Man kann Matrizen multiplizieren und erhält als Ergebnis dann wieder
eine Matrix. Dabei muss man viele Terme miteinander verrechnen: Jeder
neue Eintrag entsteht, indem man die einzelnen Werte aus der
entsprechenden Zeile der ersten Matrix nacheinander mit denen aus der
zugehörigen Spalte der zweiten Matrix multipliziert und alles
aufsummiert.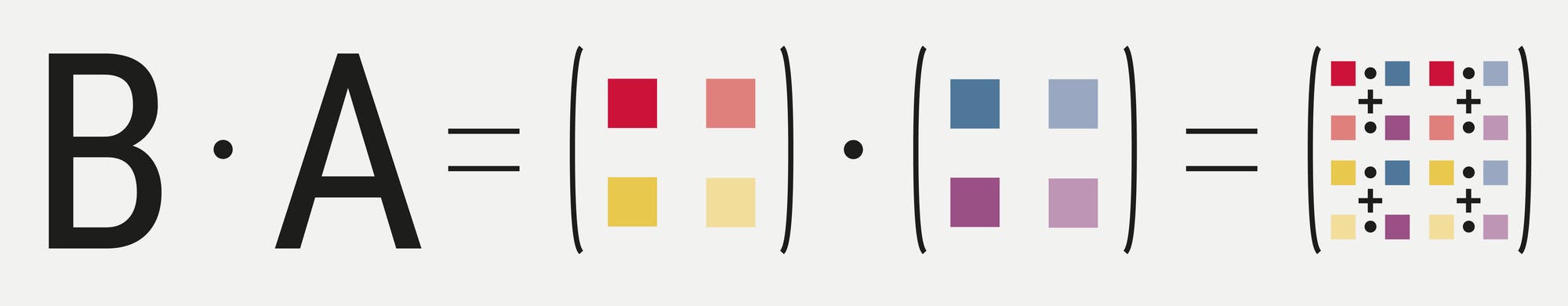
Eine Besonderheit der Matrizenmultiplikation ist, dass sie nicht
kommutativ ist. Das bedeutet, es macht einen Unterschied, ob man die
Matrix A von links oder von rechts mit B multipliziert.
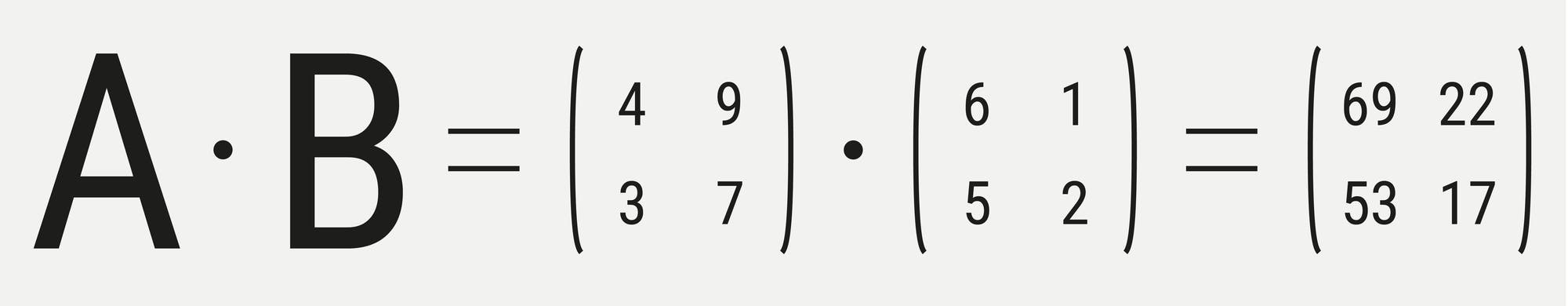
Einfach erkennen lässt sich die Nichtkommutativität am Beispiel von
Zahlen. Wenn man Matrix A von links mit Matrix B multipliziert, erhält
man für das Matrizenprodukt vier Einträge. Die
Einträge in der Matrix, die aus der Multiplikation von A und B
hervorgeht, unterscheiden sich von den Werten, die man erhält, wenn man B
mit A multipliziert. Im Allgemeinen ist bei Matrizen A mal B nicht
gleich B mal A – anders, als wir es von einfachen Zahlen kennen.
Schließlich schrieben die zwei Physiker gemeinsam mit Heisenberg im November 1925 eine Formulierung auf, die als »Dreimännerarbeit« bekannt wurde. Hier legten sie mit einer ausgearbeiteten »Matrizenmechanik« ein solides Fundament für die neue Quantenmechanik.
Wenn man aus moderner Sicht die ersten Berechnungen Heisenbergs aufs Wesentliche herunterkocht, sticht ausgerechnet die »Schwierigkeit«, die Nichtkommutativität, als wichtige Besonderheit heraus. Durch sie kommt, wenn man den Impuls p (Masse mal Geschwindigkeit) eines Teilchens mit dem Ort q multipliziert, etwas anderes heraus, als wenn man umgekehrt q mal p rechnet. Und auf geradezu magisch wirkende Weise hängt die Differenz zwischen beiden Produkten mit ebenjener Konstante h zusammen, die Planck im Jahr 1900 eingeführt hatte: pq − qp = h⁄2πi.
Auch
diese entscheidende Formel findet man am Stadtfriedhof Göttingen, wenn
man von Plancks Grab weiter zu Max Borns Ruhestätte läuft. Dort steht
sie unter Borns Namen graviert, mit ihm verbunden für die Nachwelt.
Dieser Zusammenhang war, nach Plancks Konstante, die zweite wegweisende
Erkenntnis für die Quantenmechanik: Ort und Impuls lassen sich nicht auf
klassische Weise fassen. Deswegen kann es im Quantenreich keine klar
umrissenen Bahnen geben, weder um Atome noch sonstwo.
Nichtkommutativität für die Ewigkeit | Auf dem Stadtfriedhof von
Göttingen befindet sich das Grab von Max Born. Die eingravierte Formel
unter seinem Namen, in der das plancksche Wirkungsquantum vorkommt,
drückt aus, dass quantenmechanische Größen sich nicht einfach
vertauschen lassen.
Dieses
grundlegende Prinzip führte Heisenberg bald darauf näher aus. Der
Physiker schuf damit das, wofür er heute am bekanntesten ist: die nach
ihm benannte Unschärferelation. Er stellte fest, dass miteinander
verknüpfte Größen wie p und q »simultan nur mit einer charakteristischen Ungenauigkeit bestimmt werden können«, wie er in einer 1927 publizierten Arbeit beschrieb. Auch zu dieser Einsicht gelangte Heisenberg übrigens nicht allein, sondern laut einer Fußnote durch »vielfache Anregung« seines Kollegen Wolfgang Pauli, mit dem er sich über Jahre intensiv austauschte.
Eine
Veranschaulichung des Prinzips lieferte Heisenberg gleich mit. Wenn man
beispielsweise den Aufenthaltsort eines Elektrons bestimmen möchte,
muss man hingucken. Dazu lässt man Licht auf das Teilchen fallen, denn
sonst sieht man ja nichts. Doch dadurch gibt man dem Elektron einen
Stoß, man verändert dessen Impuls. Und will man präziser messen, muss
die Energie des Lichts größer sein: »Je genauer der Ort bestimmt ist,
desto ungenauer ist der Impuls bekannt und umgekehrt.«
Das
Jahr 1925 legte also die Basis für einen konzeptionell völlig neuen,
umfassenden Blick auf die Quantenwelt. Schnell wurde der physikalischen
Gemeinschaft klar, dass dieser mathematische Weg auch praktisch
funktionierte. So berechnete Pauli mit den neuen Regeln erfolgreich die
Zustände des Wasserstoffatoms. Es ist zwar das einfachste Atom, aber es
galt bereits als notorisch schwieriger Anwendungsfall. Am Wasserstoff
musste sich jede Theorie messen lassen. Im Gegensatz zu Bohrs Atommodell
bestand die Matrizenmechanik den Test bravourös.
Urheber der Revolution war also nicht Heisenberg allein – schon gar nicht einzig sein Aufenthalt auf Helgoland. Der Held war Teil einer Heldenmaschinerie. Immerhin, das Jahr scheint gut gewählt. Oder doch nicht? Auftritt eines Widersachers.
Gerade,
als die Matrizenmechanik erste Triumphe feierte, sorgte eine andere
Interpretation der Quantenwelt für Aufsehen. Der österreichische
Physiker Erwin Schrödinger beschrieb im Jahr 1926
das Verhalten von Teilchen nicht mit unhandlichen
Matrixmultiplikationen, sondern mit Hilfe eines viel vertrauteren
Mechanismus: Schrödinger formulierte alles mit Wellen, die sich von
einem gewissen Anfangszustand an ausbreiten.
Das
hielt Einsteins Einsicht aus dem Jahr 1905 den Spiegel vor. Einstein
hatte Licht, das ehemals als Welle galt, auch Teilchencharakter
zugeschrieben. Nun begriff Schrödinger vermeintlich punktförmige
Teilchen, wie Elektronen, ihrerseits als Wellen. Die Idee hatte kurz
zuvor der französische Physiker Louis de Broglie ins Spiel gebracht.
Schrödingers Ansatz: Die Wellenfunktion des Teilchens verändert sich mit der Zeit. So lässt sich zu jedem Zeitpunkt vorhersagen, in welchem Zustand ein System ist. Das beschreibt viele physikalische Vorgänge elegant und einfach. Diese »Wellenmechanik« liefert mathematisch gesehen dieselben Ergebnisse wie die Matrizenmechanik. Das ließ sich bald darauf beweisen.
Schrödingers nachvollziehbare Wellen waren für viele Zeitgenossen reizvoller als die abstrakten Matrizen
Schrödingers
nachvollziehbare Wellen – und seine in der Physik bereits etablierten
Differenzialgleichungen – waren für viele Zeitgenossen reizvoller als
die abstrakten Matrizen. Die Wellenmechanik hatte auch praktische
Vorteile; veränderliche Prozesse lassen sich damit recht einfach
berechnen. Vieles kann man im Wellenbild leicht, geradezu intuitiv
fassen.
Allerdings
lässt sich Schrödingers Ansatz gerade deshalb als Schwäche auslegen.
Das vertraute Bild von Wellen suggeriert Anschaulichkeit – und das für
eine Welt, die doch offenbar völlig anders funktioniert als in unserer
Erfahrung. In der Wellenmechanik ist nun wieder alles auf gewisse Weise
deterministisch: Kennt man die Wellenfunktion zu einer bestimmten Zeit,
kann man sie auch für alle darauf folgenden Zeitpunkte berechnen. Für
viele wirkte Schrödingers Bild gerade deshalb so attraktiv. Wer könnte
es ihnen nach zwei Jahrzehnten verwirrender Suche nach der Natur der
Quanten verdenken?
Born schlug noch im Jahr 1926 eine eigene Interpretation vor,
die Wellen- und Teilcheneigenschaften verband. Er verwies dabei auf
eine Bemerkung Einsteins, »dass Wellen nur dazu da seien, um den
korpuskulären Lichtquanten den Weg zu weisen«.
Übertragen auf die
Quantenmechanik bedeute das: Schrödingers Wellen seien lediglich ein
»Führungsfeld«, das sich entsprechend der Schrödingergleichung im Raum
ausbreite. Es zeige den Teilchen gewissermaßen die Möglichkeiten, die
sie haben, eine Bahn einzuschlagen. Welchen Weg das Teilchen dann aber
tatsächlich nimmt und an welchem Ort es erscheint, das sei rein
zufällig. Damit gab Born die theoretische Determiniertheit der
Wellenmechanik auf, ohne auf ihren praktischen Nutzen zu verzichten. Mit
dem Ansatz lässt sich die Chance berechnen, ein Teilchen an einer
bestimmten Stelle anzutreffen: Die Amplitude der Wellen – wie stark sie
ausschlagen – liefert die Wahrscheinlichkeit dafür, das Teilchen dort zu
beobachten.<
Unerträgliche Unanschaulichkeit
Die erste radikale Aussage der Quantenmechanik war das, was etwa Planck, Einstein und Bohr früh herausgearbeitet hatten: nämlich dass die Welt im Kleinsten unteilbare Schritte macht. Revolutionärer war jedoch die Erkenntnis von Heisenberg und Born: Wohin diese Quantenschritte führen, ist unvorhersagbar.
Borns statistische Interpretation legt
schonungslos offen, was die Quantenmechanik so schwierig zu begreifen
macht. Einerseits ist aus dem Alltag völlig klar, dass sich Dinge in
einem eindeutigen Zustand befinden: Eine Katze ist entweder tot oder
lebendig, und es wäre Unsinn, zu behaupten, sie sei beides gleichzeitig.
Das ist das Argument aus Schrödingers inzwischen berühmtem
Gedankenexperiment, das er 1935 beschrieb.
Quantenmechanische Superposition
Wenn
bei einem System mehrere verschiedene Zustände möglich sind, ist laut
unserer Alltagserfahrung immer nur entweder der eine oder der andere
realisiert. In der Quantenphysik können aber auch beide gleichzeitig
vorliegen.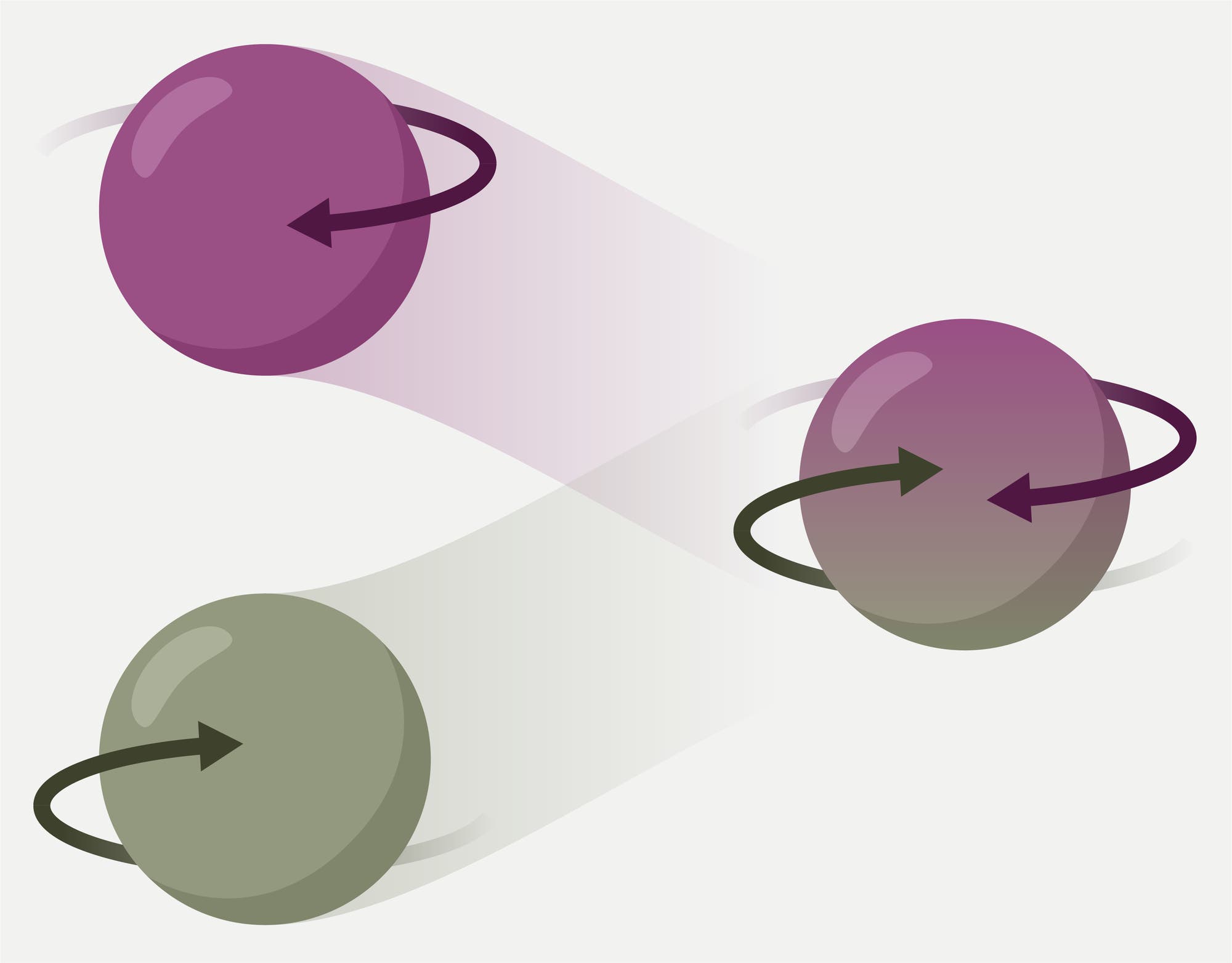 
Bei
einem solchen Überlagerungszustand hat beispielsweise der Drehsinn
eines Teilchens mehrere Werte – gewichtet mit ihrer jeweiligen
Wahrscheinlichkeitsamplitude. Erst durch eine Messung entscheidet sich,
in welchem tatsächlichen Zustand man das Quantensystem vorfindet, ob
sich das Teilchen also etwa links- oder rechtsherum dreht.
Andererseits
suggerieren uns Schrödingers Wellen, dass sich in einem Quantensystem
alles in einem Ozean der Überlagerungen unendlich vieler Zustände
befindet. Das Ganze offenbart sich mit einer gewissen Wahrscheinlichkeit
in einem konkreten Zustand erst dann, wenn wir hinschauen. Völlig
zufällig. Schrödinger wollte diese fundamental neue Unbestimmtheit nicht
akzeptieren. Auch Einstein nicht: Gott würfle nicht, schrieb er an Born
in einem oft zitierten Brief.
Erbitterte Auseinandersetzungen – bis heute
Damit
entbrannte der bislang größte Streit der Quantenmechanik. Die Fachwelt
war gespalten zwischen denen, die der von Zufall geprägten
Interpretation anhingen – gewisse Ereignisse lassen sich ganz
grundlegend auf keine Ursache zurückführen – und denen, die »verborgene
Variablen« vermuteten. Das sind unsichtbare Parameter, die Ereignisse
miteinander verknüpfen auf eine Weise, die wir bloß nicht messen können.
Irgendwelche Verbindungen muss es geben – in der Quantenmechanik heißen
sie Verschränkung.
Quantenverschränkung
In
der Quantenmechanik können in einem zusammengesetzten System mehrere
Zustände miteinander verknüpft sein – auf eine Weise, die sich klassisch
nicht erklären lässt.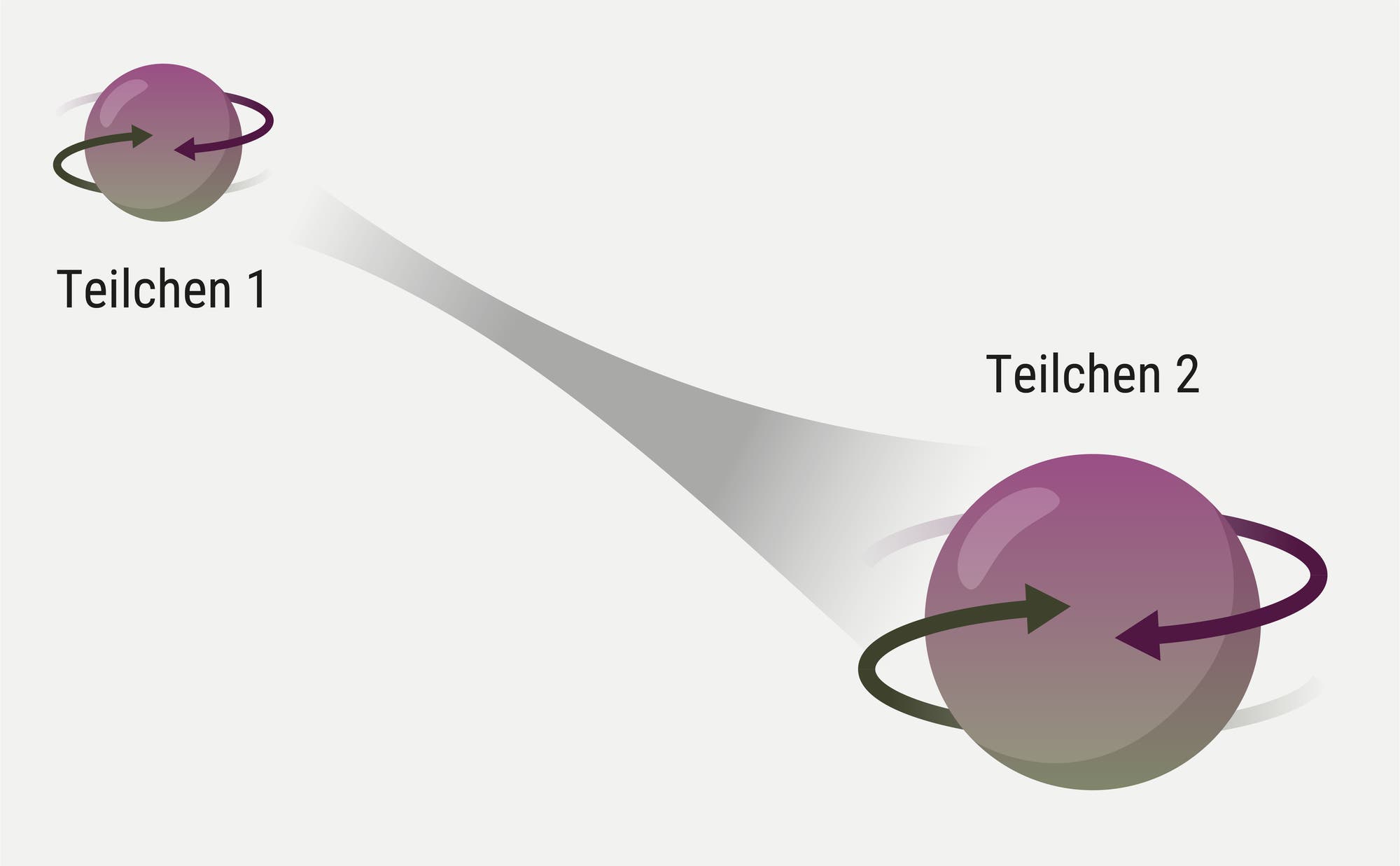 
Hier
befinden sich Teilchen 1 und Teilchen 2 jeweils in einer Überlagerung
von zwei möglichen Drehungen und sind miteinander verschränkt. Das
Besondere an der Verschränkung: Wenn man einen der beiden Partner durch
Messung auf einen eindeutigen Zustand festlegt, dann erhält auch der
andere sofort einen bestimmten Zustand.
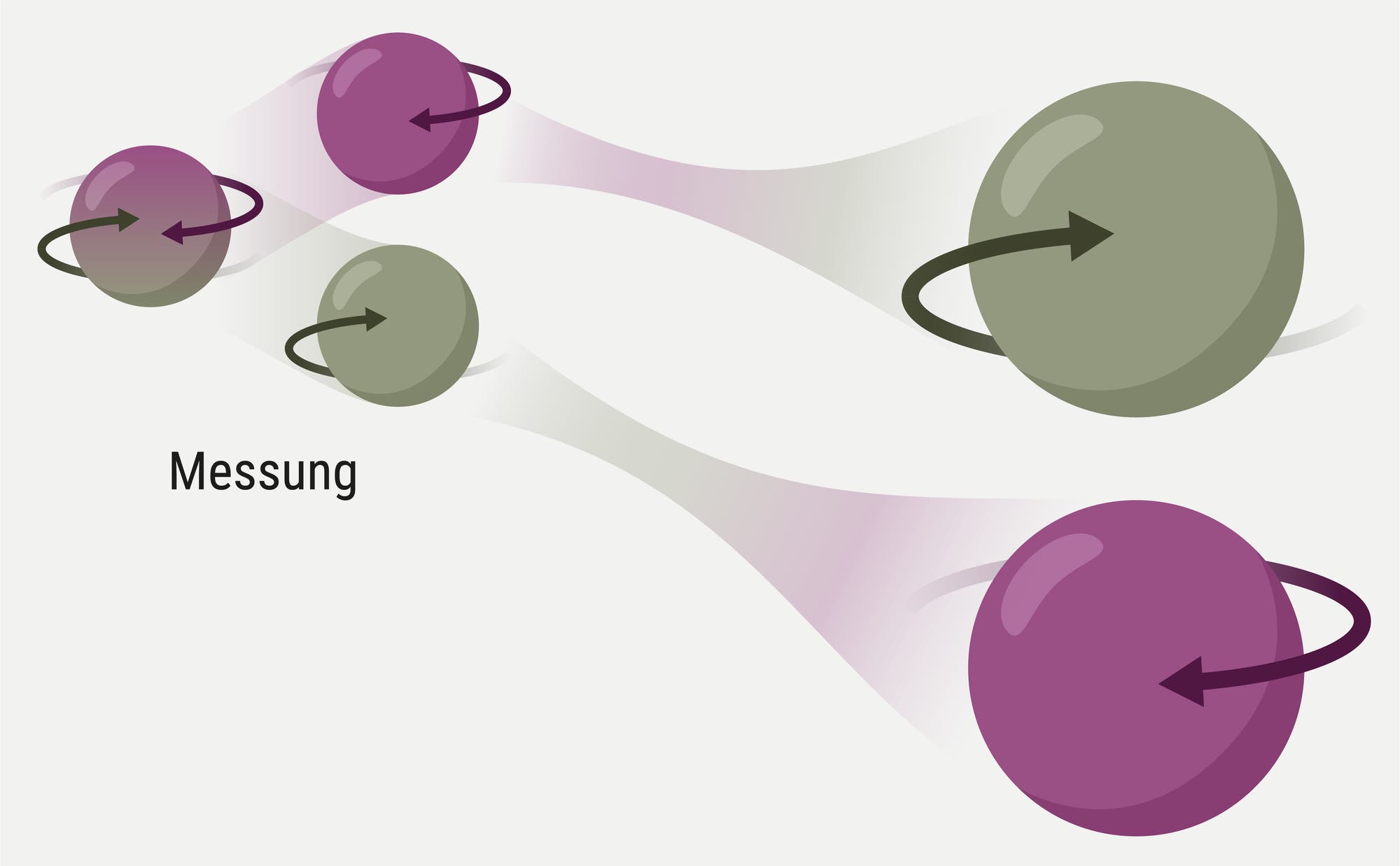
Beispielsweise
können die Drehrichtungen von Teilchen 1 und 2 so miteinander verknüpft
sein, dass Teilchen 2 stets andersherum rotiert als Teilchen 1. Dann
legt man den Drehsinn von Teilchen 1 durch eine Messung fest – und kennt
in diesem Moment zugleich den Zustand von Teilchen 2. Das gilt selbst
dann, wenn dieses sich so weit vom ersten Teilchen entfernt befindet und
seinerseits so schnell gemessen wird, dass sich beide Experimente
keinesfalls gegenseitig beeinflussen können.
Jahrzehnte später ließ sich die Existenz mancher solcher Parameter experimentell ausschließen. Dabei ging es um solche, die »lokal« sind und nur ihre unmittelbar erreichbare Umgebung beeinflussen. Heute ist klar: Teilchen können stärker miteinander verknüpft sein, als es eine lokale Theorie mit verborgenen Variablen zulassen würde. Dafür gab es im Jahr 2022 einen Nobelpreis. Doch viele Fragen zur wahren Natur der Quantenmechanik bleiben offen.
Deshalb
dauert noch heute die Diskussion darüber an. Weiterhin gibt es
Deutungen der Quantenmechanik, die auf verborgene Variablen setzen. Dann
gäbe es irgendetwas, was alles im Universum vorherbestimmt.
Dass die Quantenmechanik mitsamt ihrer Verschränkung einen
statistischen Charakter hat, sei Zeichen einer unvollständigen Theorie,
so die Anhänger dieser Sichtweise.
Welches Bild das beste ist, ist heute so wenig klar wie vor 100 Jahren
Etliche verschiedene Interpretationen der Quantenmechanik haben versucht, sich auf die seltsamen Phänomene des Mikrokosmos einen Reim zu machen. Sie sollen die zahlreichen Paradoxa auflösen, die entstehen, wenn Objekte zugleich Teilchen und Wellen sind. Oder wenn sich Zustände überlagern und offenbar erst durch Messungen festgelegt werden. Oder wenn etwas an einem Ort mit etwas anderem, weit Entferntem auf klassisch unfassbare Weise verschränkt sein kann. Welches Bild das beste ist – und ob man sich überhaupt ein Bild machen kann – ist heute so wenig klar wie vor 100 Jahren. Sicher ist seit 1925 nur: Mathematisch funktioniert alles. »Shut up and calculate!« – »Halt die Klappe und rechne!« – wurde deswegen zu einem geflügelten Wort. Das stößt vielen auf.
Denn wer diesem Mantra stur folgt, erhält zwar stets präzise Ergebnisse, erstickt aber jede kritische Auseinandersetzung, jede Suche nach Verständnis. Vielleicht auch jede Kreativität, die von jahrzehntelangen Diskursen rund um die Wunder der Quantenwelt beflügelt wurde. Philosophische Diskussionen mögen fruchtlos erscheinen, aber: Moderne Anwendungen wie Quantenkryptografie und Quantencomputer verdanken wir gerade auch dem Ausloten der Grenzen der Quantenmechanik und der experimentellen und theoretischen Suche nach Schlupflöchern.
Schon
jetzt ist absehbar, dass wir im Jahr 2035 erneut ein 100-jähriges
Quantenjubiläum feiern werden. Denn 1935 erweckte sowohl Schrödinger
seine berühmte Katze zum Leben (oder tötete sie). Zudem ging ein
weiteres Gedankenexperiment in die Geschichte ein, mit dem Albert
Einstein und seine Kollegen Boris Podolsky und Nathan Rosen 1935 zeigen
wollten, dass die Quantenmechanik unvollständig sei: Zwei weit
voneinander entfernte Teilchen könnten sich auf scheinbar unzulässige
Weise gegenseitig beeinflussen. Diese Diskussionen drehten sich längst
nicht mehr um die grundlegende Mathematik hinter der Theorie. Zehn Jahre
nach Heisenbergs Umdeutung war das kein großes Thema mehr. Stattdessen
versuchten nun alle, die Quantenmechanik zu deuten.
Während
die Welt also auf das erste umfassende Konstrukt der Quantenwelt
zurückblickt, sind die konzeptuellen Schwächen noch immer nicht
ausgeräumt. Mathematisch gesehen ist seit 100 Jahren alles klar,
anschaulich gesehen nichts. Vielleicht ändert sich das im kommenden
Jahrzehnt. Es läuft eine fieberhafte Suche nach einer Theorie der
Quantengravitation, die unsere fundamentalen Konzepte der größten und
kleinsten Skalen verbindet. Gleichzeitig kratzen immer präzisere
Experimente an den Grenzen zwischen klassischer und Quantenwelt. Damit
kommen wir eventuell einer Antwort darauf näher, was Quanten
eigentlich sind.
Im Jahr 2035 gibt es womöglich eine ganz neue Interpretation der Quantenmechanik. Wenn dann neue Heldengeschichten geschrieben werden, lohnt sich die Erinnerung an Heisenberg. Erkenntnis entstand schon damals nicht in Abgeschiedenheit. Die Natur offenbart nicht von selbst ihre geheimen, Schwindel erregend schönen mathematischen Formen. Wir entreißen sie ihr im Streit.
Manchmal brauchen wir eine eingängige Geschichte, um uns für etwas zu begeistern. Aber die vielschichtige Story hinter der Kurzversion verdeutlicht, was auch die Zukunft der Quantenmechanik prägen wird. Wenn Wissenschaft bereits vor 100 Jahren nur durch das Nebeneinander konkurrierender Ansätze, durch intensiven Austausch und leidenschaftlich geführte Debatten vorankam, dann gilt das umso mehr für die gegenwärtige Physik.
Nota. - Das sollte ich wohl besser nicht kommentieren. Ich leg mir ein wenig Zeit zurecht und lese es in aller Ruhe, und wo nötig zwei oder dreimal - und, weil ja Ferien sind, vielleicht ein paar Tage lang.
JE
Keine Kommentare:
Kommentar veröffentlichen