Ist also die Raumzeit doch gequantelt?

aus spektrum.de, 29.04.2025              Wie sieht die Raumzeit auf kleinster Skala aus?             zu Jochen Ebmeiers Realien

Kausale dynamische Triangulation
Mit dem Computer zum Ursprung der Quantenraumzeit
Ein Ansatz für eine Quantentheorie der Schwerkraft kommt ohne exotische Zutaten aus – anders als viele andere Herangehensweisen benötigt er keine mysteriösen Teilchen oder Kräfte. Zudem liefert diese »kausale dynamische Triangulation« erstaunliche Vorhersagen, etwa veränderliche Raumdimensionen.

von Renate Loll

Seit Jahrtausenden strebt die Menschheit ein ehrgeiziges Ziel an: Die gesamte Welt zu verstehen – vom Ursprung des Universums bis hin zum Ende der Zeit. Heute sind wir dabei schon weit gekommen. Aktuell deutet alles darauf hin, dass das Weltall beim Urknall hervorgegangen ist und sich seither immer weiter ausdehnt. Doch bei den Kindertagen des Kosmos versagen unsere physikalischen Theorien von Raum, Zeit und Materie. Demnach muss zu dieser Zeit alles so unvorstellbar dicht komprimiert gewesen sein, dass die etablierten Modelle die Vorgänge nicht mehr beschreiben können.

Daher versuchen Fachleute die heutigen Theorien zu erweitern, um mehr über das sehr junge Universum zu erfahren. Ging unsere Raumzeit aus einer »Ursuppe« hervor, wo Konzepte wie Kausalität und zeitliche Abfolgen nicht existierten? Liegen solche Aussagen überhaupt im Bereich der nachprüfbaren Naturwissenschaften – oder sind sie besser der Metaphysik zuzuordnen? 
 

• Sind Raum und Zeit gequantelt?
  

 
Viele Menschen sind davon überzeugt, dass nur eine Quantentheorie der Schwerkraft solche Fragen beantworten kann. In den vergangenen 100 Jahren widerstand die Gravitation aber allen Versuchen, in das Korsett der Quantenphysik gezwängt zu werden. Daher wurden Forschende kreativ und entwickelten zahlreiche Kandidaten für eine derartige vereinheitlichte Theorie. Aber bis jetzt ließ sich keine bestätigen. Ein Grund dafür ist, dass die Bereiche, in denen Quanteneffekte der Gravitation zum Tragen kommen, im Labor nicht erreichbar sind.

Daher nähere ich mich mit meinen Kolleginnen und Kollegen dem Problem aus einer anderen Richtung. Anstatt auf exotische Zutaten und spekulative Annahmen zu setzen, verwenden wir bereits etablierte Methoden aus der Quantenphysik. Wir passen sie jedoch auf die Besonderheiten der Schwerkraft an. Auf diese Weise können wir mit Computersimulationen in jene Gebiete vordringen, die für Experimente bislang unerreichbar sind. Dabei gewannen wir bereits überraschende Erkenntnisse. Diese können wir nutzen, um uns Schritt für Schritt dem endgültigen Ziel zu nähern: einer Theorie, die den Quantenursprung von Schwerkraft und Raumzeit erklären kann.

Zwei erfolgreiche, aber gegensätzliche Theorien

Im 20. Jahrhundert erschütterten zwei verschiedene physikalische Entwicklungen unser Weltbild. Die eine ist Albert Einsteins allgemeine Relativitätstheorie, die Raum und Zeit nicht mehr als unbeteiligten, starren Rahmen beschreibt. Stattdessen verschmelzen beide zu einer dynamischen Raumzeit, die sich durch die Anwesenheit von Energie und Materie verformt. Demnach entsteht die Schwerkraft und alle damit einhergehenden Phänomene durch die Krümmung der Raumzeit.

Seither haben alle verfügbaren Experimente und Beobachtungen die Vorhersagen der allgemeinen Relativitätstheorie bestätigt, von der Ausbreitung von Gravitationswellen bis hin zur beschleunigten Ausdehnung unseres Universums. Die Theorie gilt jedoch nicht auf allen Skalen. Sie stößt an ihre Grenzen, sobald die Schwerkraft und die dazugehörige Krümmung so groß werden, dass Quanteneffekte auftreten.

Teilchen unter Schwerkraft | Albert Einsteins allgemeine Relativitätstheorie besagt, dass Masse und Energie die vierdimensionale Raumzeit verformen.

Die zweite physikalische Revolution des vergangenen Jahrhunderts kam im Rahmen der Quantentheorie. Es stellte sich heraus, dass jede Art von Materie aus unteilbaren Elementarteilchen besteht. Diese verhalten sich völlig anders, als man es von der klassischen Physik gewohnt ist.

Ein einzelnes Elementarteilchen lässt sich beispielsweise nicht beschreiben wie ein punktförmiges, exakt lokalisiertes Billardkügelchen, sondern es ähnelt einer räumlich ausgedehnten Welle. Statt einer eindeutigen Position ordnet man einem Quantenteilchen daher eine Aufenthaltswahrscheinlichkeit zu. Tatsächlich folgen der Elektromagnetismus und die beiden Kernkräfte – und damit alle Grundkräfte außer der Schwerkraft – erwiesenermaßen den seltsamen Regeln der Quantenphysik.

Quantenfeldtheorie

 


Anfang des 20. Jahrhunderts entstand die Quantenmechanik – und revolutionierte die Vorstellung von Materie. Plötzlich war ein Elektron nicht mehr bloß ein punktförmiges Teilchen, sondern besaß in manchen Situationen Eigenschaften, die eigentlich lediglich Wellen innehaben. In den folgenden Jahren verallgemeinerten die Fachleute die quantenphysikalischen Konzepte, indem sie den Formalismus nicht nur auf die Mechanik, sondern auch auf den Elektromagnetismus und die Kernkräfte übertrugen.

Das führt jedoch schnell zu Problemen: Die Quantenmechanik an sich kann beispielsweise nur Systeme mit einer festen, sich nicht ändernden Teilchenzahl beschreiben, die sich nicht ändert. Im Fall des Elektrons und seines Antiteilchens, des Positrons, trifft das aber beispielsweise nicht zu. Sie löschen sich gegenseitig aus. Für solche Systeme braucht es daher eine allgemeinere Theorie.

Und so entwickelte sich die Quantenphysik weiter. In den 1950er und 1960er Jahren setzten sich so genannte Quantenfeldtheorien immer mehr durch. In diesen ist die Raumzeit niemals leer, sondern von verschiedenen Feldern durchzogen. Schwingungen darin entsprechen Teilchen oder Antiteilchen. Doch die Quantenfelder sind niemals ruhig: Sie sind der Theorie zufolge stets von kleinen Kräuselungen durchzogen, die extrem kurzlebigen Teilchen entsprechen. Die »virtuellen« Teilchen lassen sich nicht direkt detektieren – ihre Auswirkungen konnten aber bereits nachgewiesen werden.

Neben der Quantenmechanik, die Systeme mit einer bestimmten Anzahl von Teilchen beschreibt, wurde in den 1950er Jahren die relativistische Quantenfeldtheorie entwickelt. Sie umfasst auch Phänomene, bei denen sich die Teilchenzahlen verändern, das heißt bei denen etwa neue Teilchen hervorgehen. Das Standardmodell der Teilchenphysik ist eine solche Quantenfeldtheorie. Es enthält alle bisher bekannten Elementarteilchen: die Quarks, aus denen Protonen und Neutronen bestehen, sowie Leptonen, zu denen Elektronen und Myonen gehören, und darüber hinaus deren elektromagnetische schwache und starke Wechselwirkungen, die jeweils von eigenen Teilchen übertragen werden, etwa Photonen oder Gluonen.

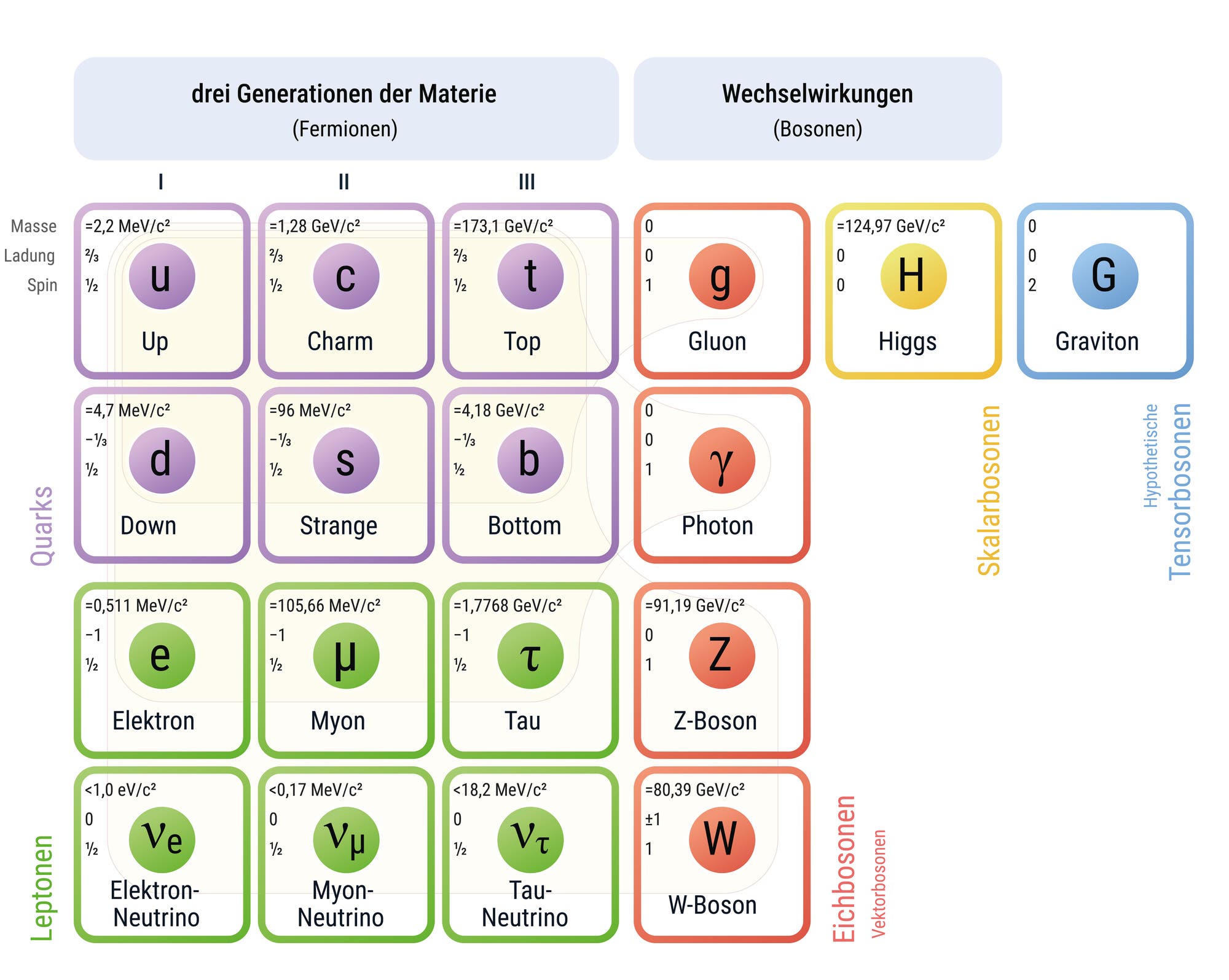
Das Standardmodell der Teilchenphysik

Standard model of elementary particles

Das Standardmodell enthält alle bisher bekannten Elementarteilchen. Links oben sind die sechs Quarks Up (u), Down (d), Charm (c), Strange (s), Top (t) und Bottom oder auch Beauty (b) verzeichnet. Sie können jeweils drei verschiedene Farbladungen besitzen (Rot, Grün oder Blau). Diese Ladung bestimmt, wie sie an Gluonen (g) koppeln, die selbst zwei Farbladungen tragen. Neben der durch die Gluonen vermittelten starken Kernkraft unterliegen die Quarks der schwachen Kernkraft und dem Elektromagnetismus. Ihre elektrische Ladung beträgt entweder 2/3 oder –1/3 der Elektronenladung. Die Masse der sechs Quarks variiert stark, vom leichtesten Up-Quark mit 2,2 MeV/c² bis zum schweren Top-Quark mit über 170 GeV/c².

Außerdem gibt es sechs verschiedene Leptonen: das Elektron (e), das Myon (μ), das Tauon oder Tau (τ) und für jedes dieser Teilchen ein dazugehöriges Neutrino (ν). Sie unterliegen alle der schwachen Wechselwirkung, und bis auf die drei Neutrinos haben sie eine negative Elektronenladung. Wie bei den Quarks schwankt auch ihre Masse: von 511 keV/c² des leichten Elektrons bis zu mehr als 1,7 GeV/c² des schweren Tauons. Die Masse der Neutrinos ist tatsächlich so klein, dass sie bisher noch nicht bestimmt werden konnte.

Quarks und Leptonen bilden zusammen drei Teilchenfamilien, die sich bis auf ihre Massen nicht voneinander unterscheiden. Sie wirken damit wie drei praktisch identische Kopien; diese Symmetrie lässt sich durch die Gruppentheorie beschreiben.

Neben den Gluonen befinden sich in der rechten Spalte die übrigen Teilchen, welche die drei Grundkräfte des Standardmodells übermitteln. Das W⁺-, das W^–- und das Z-Boson sind für die schwache Kernkraft verantwortlich, die radioaktive Zerfälle bewirkt. Das Photon übermittelt die elektromagnetische Kraft. Für die vierte Grundkraft, die Gravitation, wird vermutet, dass ein Graviton existiert. Das Higgs-Boson unterscheidet sich von seinen Artgenossen. Es hängt nicht mit einer fundamentalen Kraft zusammen, sondern verleiht den Teilchen ihre Masse. Außerdem unterliegt es der schwachen Wechselwirkung.

Um das Standardmodell zu vervollständigen, kommen noch die Antiteilchen der Quarks und der Leptonen hinzu, die sich lediglich durch das Vorzeichen ihrer elektrischen Ladung von den ursprünglichen Partikeln unterscheiden.

Die Quantennatur scheint also eine grundlegende Eigenschaft von Materie zu sein. Gleiches gilt für die Schwerkraft: Die Gravitation beeinflusst alle Formen von Materie. Das legt nahe, dass auch Phänomene der Schwerkraft den Quantengesetzen unterliegen. Doch das können wir erst dann mit Zuversicht behaupten, wenn wir eine Theorie der Quantengravitation aufgestellt haben – und ihre Vorhersagen erfolgreich getestet wurden.

Der Traum einer vereinheitlichten Theorie

Häufig heißt es, die Quantentheorie und die allgemeine Relativitätstheorie seien unvereinbar. Damit sind in erster Linie die unterschiedlichen Rollen der Raumzeit in diesen zwei Konzepten gemeint: als starre, unbeteiligte Bühne einerseits und als dynamische, wechselwirkende Größe andererseits. Allerdings gibt es bislang keine Hinweise darauf, dass diese beiden Anschauungen – und damit auch die Quantentheorie und die Schwerkraft – wirklich unvereinbar sind. Tatsächlich scheint das Gegenteil der Fall zu sein.

Eine weitere Schwierigkeit sind die unterschiedlichen Längen- und Energieskalen, bei denen die Gravitation und die übrigen drei Grundkräfte in Erscheinung treten. Bisher kam es in der Physik nie zu einem Widerspruch, weil entweder Schwerkraft oder Quanteneffekte dominieren. Damit hat sich die Frage der Vereinbarkeit in der Praxis noch nie gestellt. Möchte man beispielsweise die Bewegungen von Galaxien oder Galaxienhaufen beschreiben, ist ihre gegenseitige Gravitationsanziehung entscheidend. Bei Kollisionen in Teilchenbeschleunigern spielen hingegen lediglich Kern- und elektromagnetische Kräfte eine Rolle.

Deshalb wird der Anwendungsbereich der Quantentheorie oft als mikroskopisch bezeichnet, im Gegensatz zum kosmischen Wirkungsbereich der Gravitation. Es gibt jedoch Situationen, in denen die Gravitation und damit die Raumzeitkrümmung trotz kleinster Abstände so stark ist, dass Quanteneffekte ins Gewicht fallen. Beispiele hierfür sind das sehr frühe, dichte Universum und das Zentrum eines Schwarzen Lochs.

Solche Situationen in Laboren nachzustellen, ist bislang unmöglich. Denn die Gravitation ist deutlich schwächer als die Kräfte des Standardmodells. Typische Quanteneffekte der Schwerkraft sollten deshalb erst auf der so genannten Planckskala auftreten, bei Abständen von etwa 10^-35 Metern. Solche ultrakurzen Distanzen können selbst die leistungsfähigsten Teilchenbeschleuniger nicht auflösen.

Über kleine Quantenstörungen hinaus

Es fehlen nicht nur experimentelle Hinweise. Es gibt es auch mathematische Schwierigkeiten, die einer Quantentheorie der Schwerkraft im Weg stehen. Die störungstheoretische Methode ist eine übliche Vorgehensweise, um eine klassische Theorie durch kleine quantenmechanische Schwankungen (»Störungen«) in eine Quantenfeldtheorie zu verwandeln. Wendet man dieses Prinzip auf die Schwerkraft an, beginnt man mit einer flachen Raumzeit und fügt dann quantenmechanische Kräuselungen ein. Dabei stößt man auf Unendlichkeiten, die sich physikalisch nicht sinnvoll interpretieren lassen. Um zu einer Theorie der Quantengravitation zu gelangen, braucht es also andere unkonventionelle Methoden.

In den 1980er Jahren wurde die Stringtheorie populär, welche die Grundbausteine der Materie als winzige Fäden beschreibt, deren Schwingungen alle bekannten physikalischen Phänomene hervorrufen sollen. Ein anderer Ansatz ist die Schleifenquantengravitation, bei der die Raumzeit ein Gebilde aus kleinsten Schleifen darstellt. Solche Theorien benötigen oft zusätzliche Annahmen. Die Stringtheorie erfordert beispielsweise besondere Symmetrien oder Extradimensionen. Die hochgesteckten Erwartungen, aus ihnen Vorhersagen für messbare Quantengravitationseffekte abzuleiten, haben sich bislang nicht erfüllt.
<
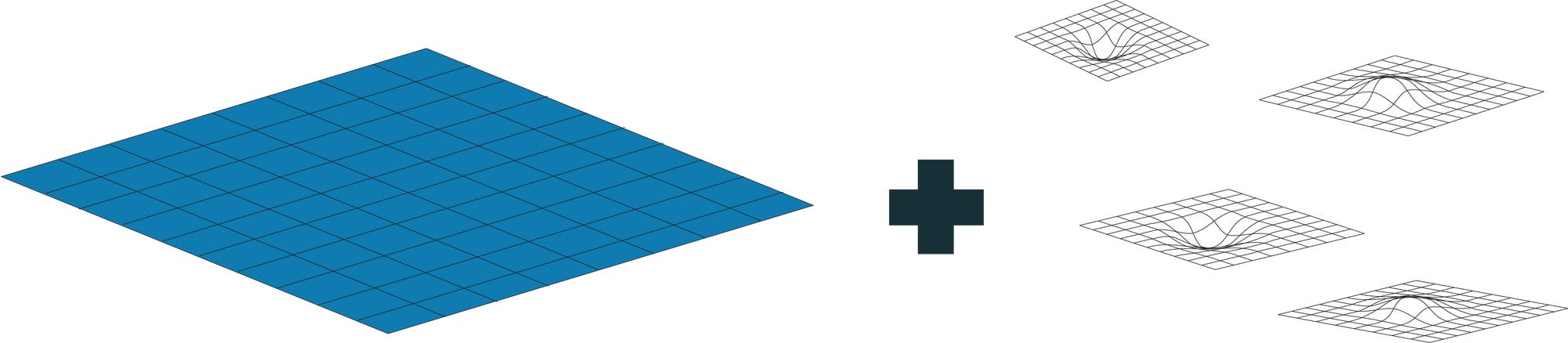
Störungstheoretischer Ansatz | Es gibt verschiedene Ansätze, um die Gravitation zu quantisieren. Eine Möglichkeit besteht darin, von einer flachen Raumzeit auszugehen und kleine Störungen hinzuzufügen.

Parallel zu diesen Ansätzen gibt es weitere Versuche, eine Theorie der Quantengravitation aufzustellen. Da bei herkömmlichen, störungstheoretischen Herangehensweisen unvermeidliche Unendlichkeiten lauern, setzen einige auf eine nicht störungstheoretische (»nicht perturbative«) Formulierung. Dabei können die quantenphysikalischen Schwankungen beliebig groß werden. Das bringt viele Vorteile mit sich, weil man dann nicht mehr nur auf kleine Quanteneffekte beschränkt ist. Allerdings sah es lange so aus, als seien effektive, nicht perturbative Rechenmethoden mit dem dynamischen Charakter der Raumzeit in der Gravitation unvereinbar.

Einen gangbaren, nicht perturbativen Weg namens »kausale dynamische Triangulierung« (kurz: KDT) habe ich mit meinen Kollegen und Kolleginnen entwickelt. Die Gravitationsfelder, die wir dabei nutzen, sind im Wesentlichen dieselben wie in der allgemeinen Relativitätstheorie. Ihr Zusammenspiel gehorcht auf kleinen Abständen allerdings den Quanten- und nicht klassischen Bewegungsgesetzen. Die Längenskalen, bei denen signifikante Quanteneffekte auftreten, sind unvorstellbar klein. Dort sind die Wechselwirkungen so stark, dass selbst Fachleute sich schwertun, ihre Dynamik zu verstehen, und sei es nur qualitativ. Glücklicherweise müssen wir uns jedoch nicht auf unsere Intuition verlassen, sondern können diese extremen Situationen mit dem Computer simulieren.

Ein Gitter bändigt die Unendlichkeiten

Als Vorbild dient eine nicht perturbative Methode, die in der starken Kernkraft genutzt wird: die Gitter-Quantenchromodynamik (kurz: Gitter-QCD). Dabei bändigt man die Unendlichkeiten der Quantenfelder, indem man die kontinuierliche Raumzeit durch ein diskretes Gitter ersetzt. Dadurch liefern alle Berechnungen endliche Ergebnisse. Diese »Regularisierung« ist nur ein technischer Zwischenschritt. Die vollständige Quantenfeldtheorie ergibt sich erst, wenn man die Gitterabstände gleichmäßig verkleinert. Dadurch wird es immer feiner, bis es die ganze Raumzeit ausfüllt.

Das quantendynamische Prinzip hinter der Gitterformulierung ist das so genannte Feynman-Pfadintegral, das in Quantentheorien oft verwendet wird. Dabei summiert man alle möglichen Quantenphänomene auf, je nachdem, wie wahrscheinlich sie sind, zum Beispiel die unendlich vielen Wege, die ein Teilchen von Ort A nach B beschreiten kann. Im Fall der Schwerkraft enthält das Pfadintegral alle möglichen Formen der Raumzeit.

Pfadintegral-Quantisierung | Um die Theorie der Schwerkraft in eine Quantentheorie zu verwandeln, kann man alle möglichen Geometrien der Raumzeit durch ein so genanntes Pfadintegral summieren.

Leider lässt sich diese in der QCD so erfolgreiche Methode nicht direkt auf die Schwerkraft anwenden, weil man sofort auf ein altbekanntes Problem stößt: Raum und Zeit spielen in der Gravitation eine völlig andere Rolle, als bei den anderen drei Grundkräften. Bei Letzteren ist die Raumzeit ein unveränderlicher Rahmen, in dem Quantenfelder existieren und miteinander wechselwirken. Der Einfluss, den diese Prozesse auf die Raumzeit selbst haben, ist komplett vernachlässigbar. Deshalb wird die Raumzeit als statisch angenommen. Dementsprechend setzt man auch In der Gitter-QCD auf ein festes Gitter, das unveränderlich ist und nicht an der Dynamik der auf ihm befindlichen Quantenfelder teilnimmt.

Im Gegensatz dazu besagt die allgemeine Relativitätstheorie, dass die Raumzeit dynamisch ist und durch Materie und Energie verformt wird. Ihre Krümmung variiert von Ort zu Ort und mit der Zeit. Um mit den gleichen Methoden eine nicht perturbative Quantentheorie der Schwerkraft zu erhalten, muss das Raumzeitgitter daher veränderlich und verformbar sein. Unsere Schlüsselidee besteht darin, die Schwerkraft auf dynamischen Gittern zu formulieren. Das webt die veränderliche Natur der Raumzeit in die Quantengravitationstheorie ein. Die KDT verknüpft somit die wirkungsvolle Technik der nicht perturbativen Gitter-QCD mit Einsteins Vorstellung einer verformbaren Raumzeit.

Dynamisch trianguliertes Gitter | Indem man ein dreiecksförmiges Gitter erzeugt, das seine Form verändern kann, lässt sich die Quantennatur der Raumzeit untersuchen.

Die Gittermethodik hat eine große Stärke: Damit lässt sich ein nicht perturbatives Pfadintegral berechnen, bei dem die Formen der Raumzeit beliebig stark von denen der allgemeinen Relativitätstheorie abweichen dürfen. Ein störungstheoretischer Ansatz würde nur kleine Veränderungen zulassen. Spannt man dann das zu Grunde liegende Raumzeitgitter immer feiner, liefert das Pfadintegral eine so genannte Quantenraumzeit. Das ist der Grundzustand der Quantengravitation, analog einem Zustand niedrigster Energie.

Die dynamischen Gitter der KDT bestehen aus identischen dreieckigen Elementarbausteinen, die kausal miteinander verknüpft werden. Jeder dieser Bausteine entspricht einem winzigen Stück Raumzeit. Genau genommen hat er die Form eines »Viersimplex«, auch Pentachoron genannt. Das ist die vierdimensionale Verallgemeinerung eines gleichseitigen Tetraeders. Das menschliche Vorstellungsvermögen stößt bei Objekten mit mehr als drei Dimensionen an seine Grenzen, aber aus mathematischer Sicht hat ein Viersimplex eine einfache Struktur.

Pentachoron | Dreidimensionale Projektion eines 5-Zellers, auch Pentachoron oder Pentatop genannt.

wesentliche Unterschied zu den Gittern, die in der Quantenfeldtheorie genutzt werden, ist aber nicht die spezifische Form der mikroskopischen Bausteine. Viel ausschlaggebender ist die Tatsache, dass sie in der KDT auf unregelmäßige Weise angeordnet sind. Im Gegensatz hierzu sind typische quantenfeldtheoretische Gitter, die eine statische Raumzeit darstellen, symmetrische Aneinanderreihungen meist viereckförmiger Bausteine.

Um das Pfadintegral zu berechnen, muss man in der KDT beliebig gekrümmte, unregelmäßige Gitter untersuchen. Aus verschiedenen Verklebungen der dreiecksförmigen Grundbausteine ergeben sich unterschiedliche Gitter. Wenn man alle von ihnen zusammenrechnet, lässt sich ihr Ensemble als Sammlung von Zufallsgittern verstehen.

Eine mikroskopische Welt ohne Koordinatensystem

Obwohl die Größe jedes einzelnen Bausteins im Grenzfall unendlich dichter Gitter gegen null schrumpft, spielt die Ordnung des zu Grunde liegenden Gitters eine wichtige Rolle. Die regelmäßigen kubischen Gitter in Quantenfeldtheorien (ohne Gravitation) eignen sich praktischerweise auch als Koordinatensysteme. Das erleichtert die Konstruktion von Messgrößen, so genannten Observablen. Sie ähneln den zweidimensionalen Koordinatensystemen, die man aus der Schule kennt, nur dass es in diesem Fall vier zueinander senkrechte Achsen gibt, eine Zeitrichtung und drei Raumrichtungen.

Bei der Quantengravitation ist das anders. Die ungeordneten Zufallsgitter der KDT lassen keine Strukturen zu, die als Koordinatensysteme dienen könnten. Das ist keine technische Unzulänglichkeit der Formulierung, sondern liegt in der Natur der Raumzeit auf der Planckskala begründet: Sie zwingt uns zu einer völlig neuen Sichtweise auf die Beschreibung der Quantenphysik.

Durch das Fehlen von Koordinatensystemen, mit denen sich Ereignisse eindeutig in der Raumzeit lokalisieren lassen, laufen sowohl die mathematischen Konstruktionen der allgemeinen Relativitätstheorie als auch unsere geometrische Anschauung ins Leere. Beide stützen sich darauf, dass man der gekrümmten Raumzeit an jedem Punkt ein virtuelles Koordinatensystem überstülpen kann, um zumindest ihre geometrischen Eigenschaften in der Umgebung dieses Punkts zu beschreiben.

Wie aber lässt sich die Quantenraumzeit untersuchen, in der das nicht funktioniert? Glücklicherweise stehen wir nicht völlig mittellos da, denn Längen- und Volumenmessungen sind noch möglich. Mit diesen elementaren Operationen ist es theoretischen Physikerinnen und Physikern gelungen, neuartige Messgrößen zu konstruieren. Doch diese unterscheiden sich stark von jenen Größen, die man aus der allgemeinen Relativitätstheorie kennt. Und wie sich herausstellt, hält ihr Verhalten einige Überraschungen bereit.

Dynamische Dimensionen

Da ein Koordinatensystem fehlt, ist das Konzept eines bestimmten Punkts in der Quantenraumzeit, den man mit Hilfe seiner Koordinaten lokalisieren müsste, bedeutungslos. Deshalb sind typische Messgrößen in der Quantengravitation »global«: Sie hängen von dem ab, was in der Quantenraumzeit als Ganzes passiert – und nicht allein von Eigenschaften in einem kleinen Gebiet.

Das erscheint auf den ersten Blick ungewöhnlich, spiegelt aber wiederum die Natur der Quantenraumzeit wider. Der Grundzustand der Quantengravitation allerdings ist starken quantenphysikalischen Schwankungen ausgesetzt und sieht überall ähnlich aus. Seine globale Dynamik geht aus dem komplexen Zusammenspiel seiner Grundbausteine hervor, das sich durch kollektive Eigenschaften und »kritische Koeffizienten« auszeichnet.

Diffusion | Die Verteilung von Tinte in einer Flüssigkeit ist im Gleichgewichtszustand (ganz rechts) am einfachsten mathematisch abzubilden.

Ein wichtiges Beispiel für solche Koeffizienten sind die Dimensionen der Quantenraumzeit. In Einsteins allgemeiner Relativitätstheorie ist der dreidimensionale Raum untrennbar mit der Zeitrichtung verbunden. Diese Vierdimensionalität ist ein fester Bestandteil der Theorie. Doch wie verhält sich das in einer Quantengravitationstheorie? Wie viele Dimensionen hat die Quantenraumzeit? Um das zu untersuchen, haben wir computergestützte Experimente entwickelt. Sie bilden das Gegenstück zu den Laborversuchen und kosmologischen Beobachtungen, welche die reale Raumzeit auf sehr viel größeren Längenskalen untersuchen.

In der KDT lässt sich die Dimension der Quantenraumzeit über einen Diffusionsprozess ermitteln. Dabei betrachtet man, wie sich eine Störung innerhalb der Quantenraumzeit ausbreitet, ähnlich wie ein Tintentropfen, den man in ein Wasserbecken fallen lässt: Es entsteht eine Tintenwolke, die sich immer weiter ausbreitet. Aus deren Volumen als Funktion der Zeit kann man auf die Dimension des Wassers rückschließen.

Als wir solche Diffusionsexperimente in der Quantenraumzeit durchführten, stießen wir auf zwei Überraschungen. Erstens ist die Dimension auf der Planckskala nicht vier, wie man erwarten würde, sondern eher (im Rahmen der Messgenauigkeit) zwei! Und zweitens hängt die Dimension von der betrachteten Längenskala ab: Zu größeren Skalen hin nähert sie sich stetig dem Wert vier.

Damit scheint einerseits die gemessene Dimension auf makroskopischen Skalen zu Einsteins Relativitätstheorie zu passen – ein Muss für jede Quantengravitationstheorie. Andererseits verdeutlicht das, dass sich die mikroskopische Quantenraumzeit nicht durch eine klassische, glatte Geometrie beschreiben lässt, die immer eine ganzzahlige Dimension hat.

Damit lieferte diese Beobachtungsgröße auf der Planckskala einen ersten Einblick in die kontraintuitiven geometrischen Eigenschaften der Quantenraumzeit. Und das war erst der Anfang.

Die Geometrie der Quantenraumzeit

Die Kunst im Bereich der KDT besteht darin, möglichst viele aussagekräftige Größen mit den dazugehörigen Computerexperimenten zu entwickeln – und die daraus gewonnenen Erkenntnisse in die Konstruktion einer Quantengravitationstheorie zurückfließen zu lassen. Dabei dienen klassische geometrische Konzepte als Inspiration, aber sie lassen sich nur selten eins zu eins auf die Planckskala übertragen.

Eine Ausnahme ist das Volumen der Quantenraumzeit. In der KDT verhält sich die Größe im Mittel wie das Volumen eines so genannten De-Sitter-Raums – eine bestimmte geometrische Form. Das ist extrem erstaunlich, da Kosmologen das frühe Universum ebenfalls als De-Sitter-Raum beschreiben. In diesem Fall ist das jedoch lediglich eine zweckmäßige Annahme, wohingegen die De-Sitter-Aspekte in der KDT aus der Quantengravitationstheorie folgen. Sie entstehen auf dynamische Weise aus dem komplexen Zusammenspiel der mikroskopischen Bestandteile der Quantenursuppe, ohne dass sie als bevorzugte Struktur hineingesteckt wurden.

Eine Größe, die sich nicht unmittelbar auf die nicht perturbative Quantentheorie übertragen lässt, ist die in Einsteins Theorie allgegenwärtige Krümmung der Raumzeit. Versucht man, die gewöhnliche Krümmung in der KDT zu berechnen, entstehen unendlich große Werte, sobald man die Gitterabstände schrumpfen lässt. Das liegt an der nicht glatten Struktur und den starken Quantenfluktuationen.

Doch im Jahr 2020 konnten wir eine Quantenkrümmung finden, die endliche Ergebnisse auf der Plancklänge liefert und auf großen Skalen mit der gewöhnlichen Krümmung glatter Räume übereinstimmt. In Computerexperimenten verhält sich die gemittelte Quantenkrümmung ähnlich wie die Krümmung eines De-Sitter-Raums. Somit haben wir einen weiteren Hinweis darauf, dass die Beobachtungsgrößen der nicht perturbativen Quantentheorie zumindest Teile der allgemeinen Relativitätstheorie reproduzieren können.

Es stellt sich also die Frage, welche Zutaten grundsätzlich nötig sind, damit aus einem Quantensubstrat eine vierdimensionale Raumzeit entsteht, die sich durch Einstein Theorie beschreiben lässt. Verhält sich vielleicht jedes System mikroskopischer geometrischer Bausteine auf der Makroebene automatisch wie unser Universum? Doch das scheint nicht der Fall zu sein.

Jahrzehntelang wurden in Studien verschiedene Zufallsgeometrien untersucht. Wie sich herausstellt, führen 99,9 Prozent dieser Modelle nicht zu einer brauchbaren Raumzeit. Diese Formulierungen können aus mathematischer Sicht interessant sein, sind aber keine Kandidaten für eine Theorie der Quantengravitation. Umso erstaunlicher ist daher der in der KDT geführte Nachweis, dass unter geeigneten Voraussetzungen eine makroskopisch vierdimensionale Raumzeit entstehen kann, die darüber hinaus konkrete Eigenschaften eines De-Sitter-Universums besitzt. Das ist ein wichtiger Hinweis darauf, dass unsere Methodik physikalisch sinnvolle Ergebnisse liefert.

Eine notwendige Zutat für eine erfolgreiche Beschreibung unseres Universums scheint eine kausale Ordnung auf den allerkleinsten Abständen zu sein, wie sie in der KDT implementiert wird. Eine solche Ordnung ist die Grundvoraussetzung für Konzepte wie Ursache und Wirkung sowie vorher und nachher. Andere nicht perturbative Ansätze der Quantengravitation vertrauen darauf, dass eine kausale Ordnung spontan aus einer Quantenursuppe ohne Zeit und Kausalität entsteht. Allerdings ließ sich ein solches Phänomen bisher noch nicht in Computerexperimenten beobachten oder anderweitig zeigen.

Keine freie Fahrt auf der Planckskala

Auch wenn die Quantengravitation selbst experimentell noch nicht zugänglich ist, heißt das nicht, dass man der Fantasie bei der Entwicklung einer entsprechenden Theorie freien Lauf lassen kann. Forschende müssen mit Computerexperimenten nachweisen, dass sich geeignete Größen wie in der klassischen Theorie verhalten, sobald man Quanteneffekte vernachlässigen kann. Zudem ist die Wahl der verschiedenen Geometrien im Pfadintegral faktisch beschränkt: Fällt der »Raum der Möglichkeiten« zu groß aus, lassen sich die Unendlichkeiten in den Berechnungen nicht beseitigen; man erhält also keine sinnvolle Theorie.

Ohne solche Realitätschecks in der Form konkreter, nicht perturbativer Berechnungen ist es auf diesem Gebiet praktisch unmöglich, Sinnvolles von Unsinn zu unterscheiden. Genau das ist jedoch sehr wichtig, um präzise Vorhersagen zu Quantengravitationseffekten zu machen – für anschließende Beobachtungen oder Experimente.

Die KDT ist in ihrer Methodik sehr einfach gehalten und kommt ohne exotische Zutaten aus. Im Gegensatz zu wesentlich komplexeren Ansätzen, die etwa auf elementaren Strings oder Schleifen aufbauen, hängt die KDT von nur zwei frei wählbaren Parametern ab: der Gravitationskonstante und einem nicht perturbativen Asymmetrieparameter. Dieser spielt in der klassischen Theorie keine Rolle, wird aber bei hohen Energien zu einer wichtigen Kopplungskonstante. Das Zusammenspiel der Quantenfelder und Wechselwirkungen ist jedoch hochkomplex und erinnert an Systeme aus der Festkörperphysik und der nicht perturbativen QCD. Speziell angepasste computergestützte Methoden sind daher unabdingbar, um die Theorie zu verstehen.

Die KDT hat uns erstmals einen Blick auf die Planckskala eröffnet. Damit liefert sie bereits jetzt konkrete Anhaltspunkte dafür, wie eine Quantenraumzeit aussehen könnte. Im Fokus steht aktuell die Frage, wie Quantenfluktuationen an verschiedenen Punkten des Quanten-De-Sitter-Universums miteinander zusammenhängen und welche Spuren sie in der kosmischen Hintergrundstrahlung hinterlassen könnten. Solche Fingerabdrücke ließen sich dann eventuell in den kommenden Jahren bei Himmelsdurchmusterungen nachweisen. Ähnlich spektakulär wäre der Beleg, dass Quanteneffekte im jungen Kosmos sich auf die Krümmung des heutigen Universums ausgewirkt haben oder sogar Strukturen hervorgerufen haben, wie wir sie anhand der heutigen Materie beobachten. Solche Forschungsansätze bieten eine hoffnungsvolle Perspektive auf die Quantengravitation – dem letzten Puzzlestück in unserem Verständnis der Grundkräfte.

 

Nota. - Ich bin kein Physiker und werde mich hüten, mich in fachliche Sachfragen einzumischen. Ich beschränke mich gebührend auf logische und... nun ja: auf 'vor-stellungslogische' Gesichtspunkte - wenn also etwa in einem theoretischen Modell zwei Vorstellungen verwendet werden, die miteinander nicht veträglich sind. Ganz ohne sachliches Verständnis geht auch das nicht, und man gerät oft in die Lage, Unfug zu reden, ohne es zu merken.

Aber dies hier ist kein Fachjournal, sondern ein ganz privates Blog. Natürlich schreibe ich gelegentlich Sachen, von denen ich die Leser überzeugen will, und argumentiere sachlich. Aber bei Gegenständen, zu denen ich keinen eigenen wissenschaftliche Zugang habe, denke ich gewissermaßen nur öffentlich nach. Kritik wäre mir willkommen, aber bedenken sie stets, dass ich all meine Sachaus-sagen stets unter Vorbehalt mache. Hier enthalte ich mich heute ihrer ganz.
JE