Quanten, Gravitation und die Weltformel.

 
aus spektrum.de, 27. 1. 2025                                                                   u Jochen Ebmeiers Realien

 

Quantengravitation: Die Suche nach einer Weltformel
Geschichte der Quantengravitation
Seit einem Jahrhundert versuchen Fachleute, die Quantenphysik mit der Schwerkraft zu vereinen. Die Geschichte ist durchzogen von vielen Durchbrüchen, Wendungen und Streitigkeiten. Ein Überblick über die Entwicklungen der wichtigsten Ansätze.

 

von Manon Bischoff

Im Sommer 1935 überraschte der Physiker Matvei Bronstein seine Professoren. Alle hatten erwartet, dass der brillante sowjetische Student eine Doktorarbeit über Halbleiter einreichen würde. Doch Bronstein entschied sich für ein völlig anderes Thema. Eines, das jeglicher Relevanz entbehrte und abwegig wirkte: Er widmete sich der Quantengravitation. Dabei kam er zu einem unerwarteten Schluss. Einsteins allgemeine Relativitätstheorie ließe sich nicht quantisieren; ein neues Konzept von Raum und Zeit müsse her. »Wer's nicht glaubt, bezahlt einen Thaler«, endet seine 1936 veröffentlichte Arbeit.

Anfang des 20. Jahrhunderts war die Physik vielen Umstürzen unterworfen. 1896 soll der Experimentalphysiker Albert Michelson noch gesagt haben, dass es in der Physik nichts Neues mehr zu entdecken gebe. Nur etwa zehn Jahre später widerlegte Albert Einstein diese Auffassung – und dabei half ausgerechnet ein zuvor von Michelson durchgeführter Versuch. Dessen Resultate konnte Einstein mit der Annahme erklären, dass Licht stets dieselbe Geschwindigkeit hat. Anschließend arbeitete Einstein den Gedanken weiter aus und zeigte: Raum und Zeit sind kein bloßer statischer Rahmen, in dem sich die Physik abspielt, sondern die beiden Größen sind untrennbar miteinander verbunden und veränderlich. Einsteins Relativitätstheorien zufolge krümmen Energie und Masse die Raumzeit und führen so zu der von uns beobachteten Schwerkraft. 

Themenwoche: Die Jagd nach der Weltformel

Die Gravitation sticht als einzige der vier Grundkräfte heraus: Anders als der Elektromagnetismus und die Kernkräfte scheint sie nicht den seltsamen Regeln der Quantenphysik zu folgen. Viele Physiker sind davon überzeugt, dass eine Theorie der Quantengravitation für ein vollumfängliches Verständnis unserer Welt nötig ist. In dieser Themenwoche beleuchten wir einige Anwärter einer solchen Theorie – und erklären, wie man sie testen könnte.

Wissenschaftsgeschichte: Die 100 Jahre lange Suche nach einer Weltformel
Schleifenqantengravitation: Das Ende der Zeit
Teleparallele Gravitation: Eine neue Raumzeit für eine Weltformel
Nichtkommutative Geometrie: Eine quantenmechanische Struktur des Kosmos
Entropie: Schwarze Löcher als Schlüssel zur Weltformel
Experimente: Folgen Raum und Zeit den Gesetzen der Quantenphysik?
Gödelsche Unvollständigkeit: Ist die Frage nach einer Weltformel unentscheidbar?

»Es gab eine Zeit, in der in den Zeitungen stand, dass nur zwölf Männer die Relativitätstheorie verstanden haben«, sagte Richard Feynman 1965. »Ich glaube nicht, dass es jemals eine solche Zeit gab. Nachdem die Leute die Abhandlung (von Einstein) gelesen hatten, haben viele die Relativitätstheorie auf die eine oder andere Weise verstanden – sicherlich mehr als zwölf.« Was die zweite große Revolution der Physik in den 1920er Jahren anging, hatte Feynman hingegen eine andere Meinung: »Ich kann wohl mit Sicherheit sagen, dass niemand die Quantenmechanik versteht.« Und diese Meinung vertreten viele Fachleute noch heute, 60 Jahre später.

Kurz nach Einsteins bahnbrechenden Erkenntnissen entstand eine neue Theorie, welche die Materie im Universum beschreibt. In dieser verschwimmen die Grenzen zwischen Wellen und Teilchen; viele Größen wie die Energie von Atomen scheinen nur noch häppchenweise (gequantelt) aufzutauchen. Und das vielleicht seltsamste Phänomen: Die Quantentheorie ist von einer grundlegenden Ungewissheit geplagt. Zahlreiche Größen lassen sich nicht mehr mit vollständiger Sicherheit bestimmen – nicht einmal mathematisch. 

• Isomorphie, das Goldene Kalb der Kosmologen.  

Albert Einstein war bereits während der Veröffentlichung seiner allgemeinen Relativitätstheorie im Jahr 1915 davon überzeugt, dass seine Theorie der Schwerkraft nicht endgültig ist und in ein allgemeineres Konzept eingebettet werden sollte. Ausschlag dafür gab unter anderem das damalige Atommodell. Anfang des 20. Jahrhunderts gingen Fachleute davon aus, dass Elektronen den Atomkern umkreisen. Das sorgt aus elektrodynamischer Sicht für Probleme, denn Ladungen auf Kreisbahnen geben Strahlung ab, wodurch sie Energie verlieren. Den Berechnungen zufolge müsste ein Elektron innerhalb von nur 10^-10 Sekunden in den Atomkern stürzen. Ein ähnliches Problem gab es auch bei Einsteins allgemeiner Relativitätstheorie: Demnach strahlt eine beschleunigte Masse (selbst eine so kleine wie die des Elektrons) Gravitationswellen aus, was ebenfalls einen Energieverlust bedingt. Allerdings ist dieser für Elektronen so gering, dass die Teilchen erst nach etwa 10³⁰ Jahren mit dem Kern zusammenprallen würden – eine Zeitspanne, die (wie wir heute wissen) die bisherige Lebensdauer unseres Universums weit übertrifft.

Das könnte Sie auch interessieren: Spektrum Kompakt Die Suche nach der Weltformel

Auch wenn Einstein mit einigen widersinnigen Konsequenzen der Quantenmechanik haderte, hatte er doch das Gebiet mitbegründet, als er feststellte, dass Licht nur gequantelt in Form von Photonen vorkommt. Er ging davon aus, dass auch die Schwerkraft im Rahmen der Quantentheorie verändert werden müsse. Während er sich fortan erfolglos um eine Erweiterung seiner allgemeinen Relativitätstheorie bemühte, zeigten sich andere Fachleute weniger besorgt.

Dass Atome eine Lebenszeit von 10³⁰ Jahren haben sollten, war mit den damaligen Modellen der Physik vereinbar. Schließlich würde man einen Kollaps höchstwahrscheinlich niemals bezeugen können. Deswegen widmeten sich die Physikerinnen und Physiker dringenderen Problemen, etwa der vollständigen Entwicklung der Quantenmechanik, die damals noch in den Kinderschuhen steckte, sowie einer Quantentheorie des Elektromagnetismus, die das Atommodell retten und erklären sollte, warum Elektronen nicht innerhalb kürzester Zeit in den Kern stürzen. »Es war ein Zeitalter des großen Umbruchs«, sagt der Wissenschaftshistoriker Alexander Blum vom Max-Planck-Institut für Wissenschaftsgeschichte in Berlin, der zu der Geschichte der Quantengravitation forscht. »Es war damals keineswegs ausgemacht, dass es die Quantenphysik auf der einen und die allgemeine Relativitätstheorie auf der anderen Seite geben würde.«

Einige Fachleute gingen davon aus, dass eine Quantentheorie des Elektromagnetismus automatisch einen Weg eröffnen würde, auch die Schwerkraft zu quantisieren – schließlich ähneln sich die Formeln beider Theorien für schwache Felder. In beiden Fällen nimmt die Kraft zwischen zwei Objekten mit quadratischem Abstand ab. So schrieben Wolfgang Pauli und Werner Heisenberg 1929 in einer Veröffentlichung zur Quantendynamik der Wellenfelder: »Erwähnt sei noch, daß auch eine Quantelung des Gravitationsfeldes, die aus physikalischen Gründen notwendig zu sein scheint, mittels eines zu dem hier verwendeten völllg analogen Formalismus ohne neue Schwierigkeiten durchführbar sein dürfte.«

Selbst wenn sich das aus heutiger Sicht als falsch erwiesen hat: Ganz Unrecht hatten die beiden Theoretiker nicht. Tatsächlich fand sich schnell eine quantisierte Version der Schwerkraft – allerdings nur für den Fall, dass die Gravitation sehr schwach ist und die Raumzeitkrümmung keine Rolle spielt. Darum dreht sich auch der erste Teil von Matvei Bronsteins Doktorarbeit: Er reproduzierte dieses Ergebnis auf elegante Weise. Im zweiten Teil seiner Arbeit untersuchte Bronstein, wie sich die Situation verändert, wenn die Schwerkraft große Werte annimmt.

Angespornt wurde er dabei von einem Fehler, den der renommierte sowjetische Physiker Lew Landau gemacht hatte. Dieser hatte fälschlicherweise behauptet, eine quantisierte Version der Elektrodynamik verhindere es, dass man das elektromagnetische Feld an bestimmten Raumpunkten messen könnte. Schnell bemerkten Fachleute den Fehler in Landaus Arbeit. Doch Bronstein erkannte, dass sich Landaus Überlegungen auf die Schwerkraft übertragen lassen. Und dort schien Landaus Argument seine Gültigkeit zu behalten: Die einsteinsche Gravitation lässt sich nicht an präzisen Raumpunkten vermessen, wenn man die Quantenphysik mit einbezieht.

Das verdeutlichte Bronstein mit einem Gedankenexperiment: Was passiert, wenn man einen winzigen Bereich der Raumzeit untersuchen möchte – sprich, das Gravitationsfeld an einem Punkt im Raum bestimmen will? Dafür kann man sich ein Mikroskop vorstellen, das immer weiter an einen Ort heranzoomt. Je feiner man den Raum abgrenzt und je kleiner die Distanz wird, die man auflösen möchte, desto größer wird laut heisenbergscher Unschärferelation der Impuls im beobachteten Bereich. Die Unschärferelation verknüpft beide Größen miteinander. Je präziser man die eine kennt, desto ungenauer wird die andere. Diese Unsicherheit wächst immer stärker an, wodurch der Impuls (und damit die Energie) irgendwann so groß wird, dass, wie wir heute wissen, ein Schwarzes Loch entstehen würde. Das verhindert jede Vermessung des Bereichs. Verbindet man Quantentheorie und allgemeine Relativitätstheorie, ergibt sich eine natürliche Barriere, die es verhindert, die Geometrie eines Punkts genau aufzulösen. »Es ist kaum möglich, die Quantengravitationstheorie auf diesen Bereich auszudehnen, ohne die klassischen Konzepte gründlich zu überarbeiten«, schloss Bronstein daher in seiner Arbeit. Man müsse sich deshalb von der riemannschen Geometrie, auf der die allgemeine Relativitätstheorie aufbaut, und von dem bisherigen Bild der Raumzeit verabschieden.

Allgemeine Relativitätstheorie | Mit seiner allgemeinen Relativitätstheorie beschrieb Albert Einstein die Schwerkraft als Folge einer gekrümmten Raumzeit.

Dieses Fazit erscheint heute radikaler als zur damaligen Zeit. Die physikalische Welt hatte gerade mehrere Umstürze erlebt, was einen solchen Perspektivwechsel nicht so außergewöhnlich machte. Doch die Fachwelt, die mit anderen Fragestellungen beschäftigt war, widmete Bronsteins Ergebnissen nur wenig Aufmerksamkeit. »Bronstein war ein historischer Ausreißer«, sagt Blum. »Im Nachhinein wird er oft als Visionär bezeichnet, aber es gab damals noch nicht die theoretischen Grundlagen, um seine weit reichende Aussage zu untermauern. So gab es zu Bronsteins Zeiten das Konzept des Schwarzen Lochs noch gar nicht.« Sein Gedankenexperiment sei zwar nachvollziehbar, aber es fehlte ein solider Ansatz, der Quantenphysik und allgemeine Relativitätstheorie miteinander vereint, an dem das exemplarisch gezeigt wird. Leider blieb dem Physiker trotz seines jungen Alters kaum noch Zeit, seine weitere Arbeit fortzuführen: 1937 wurde Bronstein im Zuge der stalinistischen Säuberungen im Alter von 30 Jahren verhaftet und kurz darauf getötet.

Mit diesem tragischen Ende lag auch das Gebiet der Quantengravitation gute 15 Jahre lang brach. Erst in den 1950er Jahren kam der Physiker John Wheeler auf ähnliche Schlüsse wie Bronstein, ohne von dessen Arbeiten gewusst zu haben. In dieser Zeit keimten drei grundlegend verschiedene Ansätze für eine Theorie der Quantengravitation auf, die in abgewandelter Form bis heute verfolgt werden. Mehrmals schien es, als stünde eine ausgearbeitete Theorie kurz bevor – doch jedes Mal gab es herbe Rückschläge, so dass bis heute eine quantenphysikalische Theorie der Schwerkraft fehlt.

Erste Schritte in Richtung Quantengravitation

Bereits in den 1930er Jahren hatten Bronstein und andere Kollegen den Fall einer flachen Raumzeit, also schwacher Gravitation, untersucht und quantisiert. Um auch die Raumzeitkrümmung in diesen Ansatz einzuführen, fügten Fachleute zunächst kleine Schwankungen zur flachen Geometrie hinzu. Ziel war es, diese Änderungen durch eine Quantentheorie auszudrücken. Das ist ein beliebter Ansatz in der Physik, der als Störungstheorie bezeichnet wird: Man beginnt mit dem denkbar einfachsten Spezialfall, der sich meist noch exakt lösen lässt (in diesem Fall die flache Raumzeit), und fügt dann nach und nach kleine Abweichungen hinzu, um kompliziertere Fälle zu betrachten.

Schnell fiel auf, dass sich die kleinen Störungen der flachen Raumzeit durch ein bestimmtes Teilchen beschreiben lassen, das so genannte Graviton. In diesem Bild ergibt sich die gekrümmte Raumzeit der allgemeinen Relativitätstheorie durch eine flache Geometrie, die durch das Graviton verformt wird. Ergebnisse dieses Wegs sollten sich in den 1980er Jahren schließlich mit der Stringtheorie verbinden lassen.


Renormierung | Messgrößen wie die Ladung eines Teilchens entsprechen nicht ihren tatsächlichen (»nackten«) Werten. Weil das Vakuum nicht leer ist und aus vielen kurzzeitig erscheinenden Teilchen-Antiteilchen-Paaren besteht, schirmen diese die Ladung eines Elektrons ab. Je mehr man sich dem Teilchen nähert, desto größer erscheint sie. Solche Effekte muss man berücksichtigen, wenn man die Gleichungen der Quantenfeldtheorien auswertet.

Einen anderen Ausgangspunkt für eine Quantengravitationstheorie bietet die so genannte kanonische Quantisierung. In diesem Fall wird die Raumzeit nicht in zwei Versionen (flach plus Störung) aufgeteilt, sondern soll als Gesamtes quantisiert werden. Dafür braucht man die grundlegenden Größen einer Theorie, etwa die Energiefunktion und einige Beobachtungsgrößen, und drückt diese quantenmechanisch aus. Auf diese Weise fließen die Unschärferelationen sowie die häppchenweise auftretenden Werte, die charakteristisch für die Quantenphysik sind, in die ursprünglich klassische Theorie ein. Ziel des kanonischen Ansatzes ist es, eine Art Schrödingergleichung zu finden, welche die zeitliche Entwicklung eines Systems beschreibt. Im Fall der Schwerkraft entspricht das betrachtete System aber nicht irgendwelchen Teilchen, sondern der Raumzeit. Dieser Ansatz führte in den 1980er Jahren schließlich zur Schleifenquantengravitation.

Der dritte Ansatz beruht auf so genannten Pfadintegralen. Bei dieser Methode erhält man eine Quantentheorie, indem man alle verschiedenen Möglichkeiten, wie sich ein System verändern kann, addiert. Für eine Quantengravitationstheorie müsste man daher alle möglichen Formen der Raumzeit summieren, um daraus abzuleiten, wie sich das Universum entwickelt. Dieser Zugang führte später zu Ansätzen wie der kausalen dynamischen Triangulation.

Damit hatten die Fachleute drei grundlegend verschiedene Wege, die sie für eine Theorie der Quantengravitation verfolgen konnten. Mittels aller drei Methoden lässt sich die Mechanik in die Quantenmechanik überführen. Entsprechend waren die Fachleute Ende der 1950er Jahre hoffnungsvoll, dass zumindest einer der Ansätze bei der Gravitation funktionieren würde. Und tatsächlich sahen die Ergebnisse in den folgenden zehn Jahren viel versprechend aus.

So konnte Feynman die ersten Quanteneffekte aus dem störungstheoretischen Ansatz ableiten. Zudem gelang es im Fall der kanonischen Quantisierung, die Energiefunktion aus Einsteins ursprünglichen Feldgleichungen der allgemeinen Relativitätstheorie herzuleiten. Es schien nicht mehr viel für eine funktionierende Theorie der Quantengravitation zu fehlen.

Die Abwärtsspirale

Doch dann kamen die Rückschläge. Denn der störungstheoretische Ansatz führt bei allen Quantenfeldtheorien zu Problemen: In den mathematischen Termen tauchen unweigerlich Unendlichkeiten auf. Die Physiker Gerardus t'Hooft und Martinus Veltman untersuchten in den 1970er Jahren, wie sich diese Unendlichkeiten beheben lassen. Statt sich direkt der störungstheoretischen Gravitation zu widmen, begannen sie ihre Analyse an so genannten Yang-Mills-Theorien, zu denen unter anderem das Standardmodell der Teilchenphysik zählt. Es sollte eine Art Aufwärmübung sein.

Die beiden Forscher bewiesen, dass Yang-Mills-Theorien »renormierbar« sind. Das heißt: Indem man einige als konstant angenommene Werte wie die Elektronenmasse, Elektronenladung und die Wechselwirkungsstärke als veränderlich ansieht, lassen sich die Unendlichkeiten beseitigen. Was wie ein seltsamer Trick wirkt, lässt sich physikalisch rechtfertigen.

Wenn man die Ladung eines Elektrons bestimmt, tut man das in der Regel aus der Ferne. Nähert man sich dem Elektron an, spielen Quanteneffekte eine Rolle. Laut der Quantentheorie ist der leere Raum nie wirklich leer, ständig entstehen Teilchen-Antiteilchen-Paare, die sich sogleich wieder vernichten. In der unmittelbaren Umgebung eines Elektrons schwirren diese Paare herum und richten sich so aus, dass ihre Ladungen die des Elektrons abschirmen. Je weiter man sich einem Elektron also nähert, als desto größer stellt sich dessen wahre Ladung heraus. Demnach variiert die wahrgenommene Ladung eines Teilchens mit der Distanz, aus der man es betrachtet. Indem man das beachtet, verschwinden die Unendlichkeiten der störungstheoretischen Yang-Mills-Theorie.

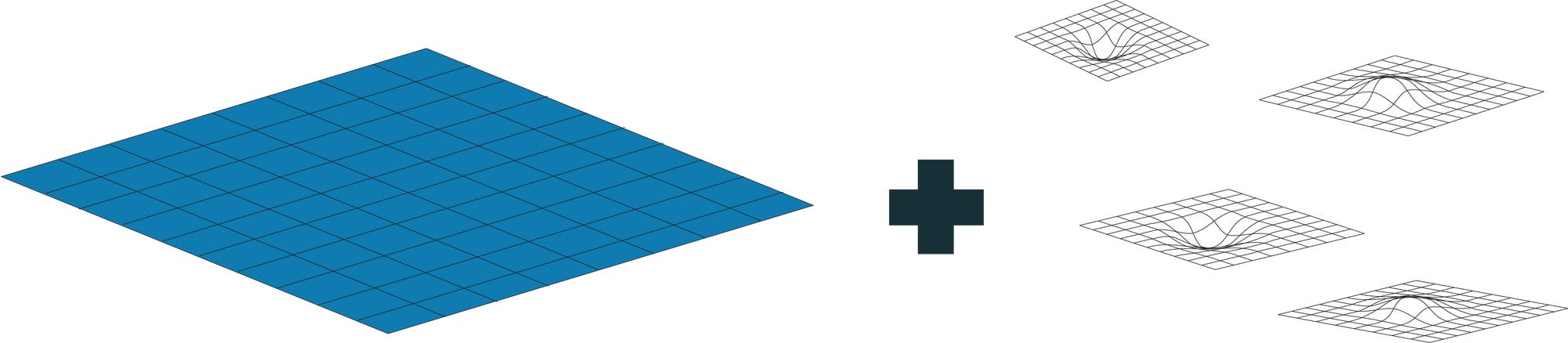
Störungstheoretischer Ansatz | Es gibt verschiedene Ansätze, um die Gravitation zu quantisieren. Eine Möglichkeit besteht darin, von einer flachen Raumzeit auszugehen und kleine Störungen hinzuzufügen.  vgl. hier

Die Unendlichkeiten zeigen in diesen Fällen also nur an, dass etwas Wichtiges nicht bedacht wurde. Mit Hilfe der Renormierung konnten 't Hooft und Veltman viele Quantenfeldtheorien vor dem Untergang retten. Für dieses Ergebnis ihrer Aufwärmübung erhielten sie im Jahr 1999 den Nobelpreis für Physik.

Doch als die beiden Physiker im Jahr 1974 die störungstheoretische Gravitation mit ihrem Renormierungsformalismus untersuchten, stießen sie auf eine unangenehme Überraschung. Die unendlich großen Terme scheinen niemals zu versiegen. Wie sich herausstellt, müsste man unendlich viele Variablen renormieren, damit die Theorie endlich bleibt. Damit war klar: Die allgemeine Relativitätstheorie ist aus störungstheoretischer Sicht nicht renormierbar – die Unendlichkeiten bleiben immer bestehen. Das versetzte dem Ansatz, bei dem kleine Störungen einer flachen Raumzeit hinzugefügt werden, den Todesstoß. Die einzige Möglichkeit, diese Methode zu retten, besteht darin, eine neue Theorie der Schwerkraft zu finden.

Auch der kanonische Zugang zur Quantengravitation mündete in den 1970er Jahren in eine Sackgasse. Bei diesem Ansatz versuchte man, anhand der Energiefunktion eine Art Schrödingergleichung aufzustellen, mit der sich die zeitliche Entwicklung des Universums berechnen lässt. Dazu stellten sich die Fachleute einen extrem abstrakten Raum vor, dessen Punkte jeweils einer möglichen Geometrie der Raumzeit entsprechen. Die Energiefunktion sollte bestimmen, wie man sich durch diesen Raum bewegt, also wie sich die Geometrien der Raumzeit nach und nach verändern.

Bei den übrigen Grundkräften erwies sich der kanonische Ansatz als erfolgreich. Allerdings nimmt die Energiefunktion für die allgemeine Relativitätstheorie eine völlig andere Form an als in den anderen Fällen. Durch die vielen Symmetrien der Raumzeit gibt es beispielsweise etliche Wahlfreiheiten, gleichzeitig müssen die Formeln für eine passende Theorie zahlreiche Bedingungen erfüllen. Als Fachleute diese auswerteten, stellten sie mit Erschrecken fest, dass die Zeitvariable aus den Formeln verschwindet. Demnach gibt es in der Theorie keine Zeitentwicklung. Tatsächlich gilt das bereits für die klassische Theorie der Schwerkraft, nicht für die quantisierte. Das löste Diskussionen darüber aus, ob man sinnvolle Physik ohne eine zeitliche Größe machen könnte.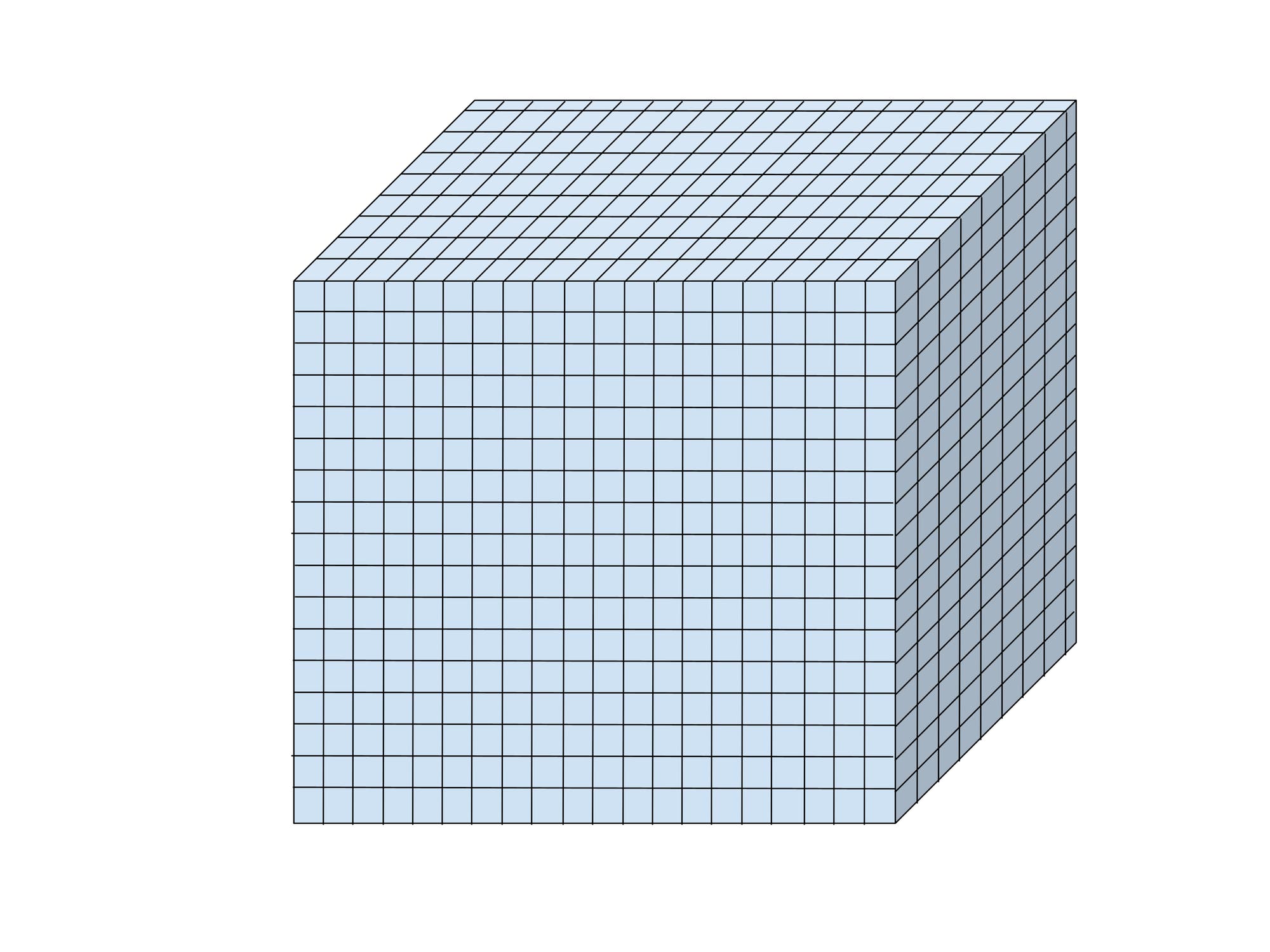


Kanonischer Ansatz | Beim kanonischen Zugang zu einer Quantengravitationstheorie wird der der so genannte Zustandsraum in kleine Häppchen (hier: Würfel) aufgeteilt. Jeder Punkt im Zustandsraum entspricht einer bestimmten Form, welche die Raumzeit annehmen kann.

Nur beim dritten Ansatz der Quantengravitation, dem Feynman-Pfadintegral, gab es zu jener Zeit Fortschritte, die Hoffnung aufkommen ließen. Verantwortlich dafür war vor allem Stephen Hawking, der Quantenteilchen in einer gekrümmten Raumzeit untersuchte. Dabei erkannte er, dass sich die Summe über alle Raumzeitgeometrien sehr einfach berechnen lässt, wenn man vier Raumkoordinaten statt einer Zeit- und drei Raumkoordinaten betrachtet. Was zunächst viel versprechend wirkte, führte allerdings auch in einer Sackgasse. Denn der Ansatz ließ sich nicht für Systeme mit einer zeitlichen Koordinate verallgemeinern.

Damit steckte die Quantengravitation Ende der 1970er Jahre in einer Krise. Und es war keine naheliegende Lösung in Sicht.

Neue Hoffnung keimt auf

Mitte der 1980er Jahre schien sich das Blatt zu wenden. Nachdem der störungstheoretische Ansatz begraben wurde, erwachte eine alte Idee wieder zum Leben: die der Stringtheorie, eine Quantentheorie von eindimensionalen Fäden, die sich durch die Raumzeit bewegen. Fachleute hatten dieses Modell zwei Jahrzehnte zuvor genutzt, um zu beschreiben, wie Protonen und Neutronen im Atomkern miteinander wechselwirken. Diese Form der Stringtheorie wurde jedoch durch die Quantenfeldtheorie der starken Kernkraft abgelöst, die Quantenchromodynamik.

Den Forschenden war jedoch aufgefallen, dass die Fäden in der Stringtheorie nicht nur die Verbindung von Quarks modellieren, sondern manche Schwingungen der Objekte die Eigenschaften eines Gravitons aufweisen. So keimte die Hoffnung auf, dass auch die anderen Teilchen – Quarks, Gluonen, Elektronen und so weiter – aus den verschiedenen Vibrationen der Strings hervorgehen könnten. Und es schien, als ließe sich die Theorie renormieren. Das war die Geburtsstunde der Stringtheorie als Kandidat für eine Weltformel. Die Stringtheorie beschreibt eine kontinuierliche Raumzeit, in der sich die eindimensionalen Fäden bewegen, und kann einige Ergebnisse der störungstheoretischen Quantengravitation reproduzieren, die Feynman vorangetrieben hatte.

Tatsächlich geht die Stringtheorie weit über den störungstheoretischen Ansatz hinaus. Anstatt bloß eine Quantenversion der Schwerkraft zu bieten, könnte sie alle Grundkräfte miteinander vereinen. Dass sich die Gravitation vielleicht nur in Verbindung mit den anderen Kräften quantisieren lässt, ist nicht völlig abwegig: Die Quantenfeldtheorie der schwachen Kernkraft lässt sich beispielsweise nur in Kombination mit der Elektrodynamik entwickeln. So erhält man die elektroschwache Theorie.

Schnell tauchten aber erste Schwierigkeiten auf. Die Stringtheorie funktioniert beispielsweise nur mit einer zehn- oder höherdimensionalen Raumzeit. Da wir nur drei Raumdimensionen wahrnehmen, schlossen die Fachleute, dass die übrigen sechs ganz klein aufgewickelt sein müssten. Je nachdem, zu welcher Form sie komprimiert sind, ergeben sich andere Gesetzmäßigkeiten. Aufgabe ist es daher, jene Formen zu finden, die zu unserer beobachteten Welt passen. Die Theorie hat weitere Überraschungen parat: Sie sagt zu jedem der bekannten Elementarteilchen ein Partnerteilchen voraus, von denen bisher noch kein einziges beobachtet wurde. Dennoch stieg das Interesse an der Stringtheorie in den 1980er Jahren stark an, als klar wurde, dass sie offenbar eine störungstheoretische Formulierung erlaubt.

 

Pfadintegral-Quantisierung | Um die Theorie der Schwerkraft in eine Quantentheorie zu verwandeln, kann man alle möglichen Geometrien der Raumzeit durch ein so genanntes Pfadintegral summieren.

Zugleich erlebte auch der kanonische Ansatz einen Aufschwung, als der Physiker Abhay Ashtekar eine neue Möglichkeit fand, um die Zeitentwicklung in der allgemeinen Relativitätstheorie zu untersuchen. Anstatt einen abstrakten Raum mit allen möglichen Geometrien einer Raumzeit zu untersuchen, wandte sich Ashtekar einer anderen Größe zu, dem so genannten Zusammenhang. Dieser beschreibt, wie sich ein Vektor (oft als Pfeil dargestellt) ändert, wenn man ihn entlang einer gekrümmten Oberfläche bewegt. Über den Zusammenhang lässt sich die Krümmung der Raumzeit ermitteln, die in der Mathematik üblicherweise durch die so genannte Metrik beschrieben wird. Durch diesen Wechsel von der Metrik zum Zusammenhang erkannte Ashtekar, dass die Energiefunktion und der zu Grunde liegende Raum, durch den die verschiedenen Geometrien des Universums codiert sind, einer Quantentheorie ähneln.

Den endgültigen Durchbruch beim kanonischen Ansatz lieferte ebenfalls eine ältere, bereits verworfene Theorie. Der Physiker und Nobelpreisträger Kenneth Wilson hatte 1974 Schleifen eingeführt, um die Vorgänge der starken Kernkraft jenseits der Störungstheorie zu beschreiben – also dann, wenn die starke Kernkraft wirklich stark ist. Wie sich herausstellte, führt das mathematische Konzept der Schleifen auf einer flachen Raumzeit jedoch zu Problemen. Die Physiker Ted Jacobson und Lee Smolin erkannten 1988, dass diese Schleifen für eine Theorie der Schwerkraft funktionieren, die ohne eine zu Grunde liegende Raumzeit auskommt, sondern die Raumzeit selbst beschreibt. Indem man den abstrakten Raum durch Schleifen ausdrückt, lässt sich die Theorie quantisieren. Damit war die Schleifenquantengravitationstheorie geboren.

Auf Basis dieser neuen Formulierung ließen sich 1992 erstmals konkrete Berechnungen durchführen. So leitete der Physiker Carlo Rovelli zusammen mit Ashtekar und Smolin die Struktur der Raumzeit gemäß der Theorie her. Demnach besteht sie aus einer Art Gewebe mit schaumartiger Struktur. Damit sagt die Schleifenquantengravitation eine diskrete Raumzeit voraus. Wenige Jahre später zeigten Forschende, dass gewisse geometrische Größen wie Flächen oder Volumen nur häppchenweise vorkommen, also quantisiert sind.

Auch im dritten Bereich, der Pfadintegral-Quantisierung, gab es in den 1990er Jahren Fortschritte. Der mathematische Physiker Edward Witten, der im Bereich der Stringtheorie forscht, quantisierte eine dreidimensionale Version der allgemeinen Relativitätstheorie (mit nur zwei Raum- und einer Zeitdimension) mit Hilfe der Pfadintegrale.

Erste Vorhersagen

Zu jener Zeit lieferten die verschiedenen Ansätze der Quantengravitationen erste Ergebnisse. Wieder keimte die Hoffnung auf, eine vereinheitlichte Theorie könnte kurz bevorstehen. Doch wie in den Jahrzehnten zuvor gab es auch dieses Mal Rückschläge.

Mit fortschreitender Computerleistung entwickelte sich aus dem Pfadintegral-Ansatz ein neues Gebiet: das der kausalen dynamischen Triangulation. In diesem werden, wie zuvor auch, alle möglichen Raumzeitgeometrien summiert. Allerdings gehen die Fachleute dabei nicht von einer kontinuierlichen Struktur aus, sondern von einer gekörnten. Die Raumzeit wird durch eine Art Gitter aus winzigen Dreiecken angenähert, damit sie ein Computer verarbeiten kann.

Auch bei der Stringtheorie und der Schleifenquantengravitation gab es einen Durchbruch – bemerkenswerterweise fast gleichzeitig. 1996 konnten beide Theorien ein zentrales Ergebnis reproduzieren, das Stephen Hawking in den 20 Jahre zuvor bewiesen hatte. Als Hawking das Verhalten von Quantenteilchen in stark gekrümmten Räumen rund um Schwarze Löcher untersucht hatte, erkannte er – zusammen mit seinem Kollegen Jacob Bekenstein – eine seltsame Eigenschaft von Schwarzen Löchern, die sie von allen anderen Objekten im Universum zu unterscheiden scheint: Ihre Entropie wächst mit ihrer Fläche statt ihrem Volumen. Seither war klar, dass eine Theorie der Quantengravitation dieses Resultat liefern muss. Dass sowohl die Stringtheorie als auch die Schleifenquantengravitation dieses Verhalten vorhersagen, löste großen Enthusiasmus aus.

Doch die Zeit der gemeinsamen Feierlichkeiten währte nicht lange. Denn schon bald brach einer der größten Konflikte aus, den die Welt der Physik je gesehen hat.

Die friedlichen Zeiten sind vorbei

Seit ihren Anfängen in den 1980er Jahren wuchs das Feld der Stringtheorie in den USA sehr schnell an – viel rascher als die anderen Ansätze für Theorien der Quantengravitation. »Das liegt unter anderem an den Grundlagen der Stringtheorie, die von der Teilchen- und Hochenergiephysik kommen«, erklärt Blum. Durch das Manhattan-Projekt hatte die Politik ein großes Interesse an Forschung in diesen physikalischen Bereichen und förderte entsprechende Vorhaben. »In den 1970er Jahren war die Arbeit am Standardmodell der Teilchenphysik so gut wie abgeschlossen«, sagt Blum. Viele Fachleute suchten nach neuen Herausforderungen und wandten sich daher der Stringtheorie zu. So wuchs der Bereich zu einem »übermächtigen Apparat« an, führt Blum aus: »Die Community der allgemeinen Relativitätstheorie, aus der letztlich die Schleifenquantengravitation entstand, war zum Beispiel viel kleiner.«

Trotz ihrer Größe war die Stringtheorie nicht von Erfolgen gekrönt, sondern machte schwer wiegende Probleme: Die Vorhersagen deckten sich nicht mit den Messungen. Zum Beispiel sagte die Theorie eine »R-Symmetrie« voraus, die sich durch bestimmte Teilchenzerfälle äußern sollte. In Experimenten konnten diese allerdings nicht nachgewiesen werden. Also veränderten Stringtheoretiker ihre Modelle, damit sie wieder zu den Beobachtungen passten. Gleiches geschah, als die vorhergesagten Partnerteilchen ausblieben. Stets schien es eine Stellschraube zu geben, an der man drehen konnte, um die erwarteten Belege zu rechtfertigen. Einige Kritiker zweifelten daher zunehmend an der Wissenschaftlichkeit des Bereichs überhaupt.

Und auch die zehndimensionale Raumzeit, welche die Theorie vorhersagt, wuchs 2003 zu einem weitaus größeren Problem an als geahnt. Wie sich damals herausstellte, gibt es extrem viele verschiedene Möglichkeiten – etwa 10⁵⁰⁰, wie die überschüssigen Raumdimensionen aufgerollt sein könnten. Jede entspricht einer Beschreibung eines Universums. »Das Problem ist nicht unbedingt die schiere Anzahl«, sagte die Physikerin Sabine Hossenfelder zu Arte, »sondern dass bisher keine Lösung gefunden wurde, die unserem Universum entspricht.« Da sich bisher nicht bestimmen lässt, welche Variante mit unserer Welt übereinstimmt, sagen manche Stringtheoretiker, dass sie alle realisiert sein könnten – und wir in einem Multiversum leben.

Trotz all dieser Rückschläge hatten zahlreiche Stringtheoretiker wissenschaftliche Lehrstühle an Universitäten inne, produzierten viel zitierte Veröffentlichungen, bekamen Forschungsgelder und gewannen Preise. Allerdings sind die Ressourcen in der Wissenschaft – insbesondere in der Grundlagenphysik – stark begrenzt. Kein Wunder also, dass schon bald ein Streit ausbrach.

»Das wird einfach immer unverschämter und lächerlicher«, beschrieb Peter Woit seine Gedanken, die er im Jahr 2004 hatte, im Magazin »Nautilus«. Er startete damals einen Blog, in dem er Kritik an der Stringtheorie übte. »Es gab diese riesige öffentliche Werbung für die Theorie, all diese Aussagen, wie wunderbar die Stringtheorie ist … Doch sie funktionierte nicht.« Sein Hauptkritikpunkt war – und ist noch heute, dass die Theorie keine überprüfbaren Vorhersagen macht.

Die Situation eskalierte, als 2006 zwei Bücher erschienen, die aus diesem Grund hart mit der Stringtheorie ins Gericht gingen: »Not even wrong« von Woit und »The trouble with physics« von Smolin. Die Reaktionen ließen nicht lange auf sich warten. Einige Stringtheoretiker reagierten heftig auf die beiden Werke. Besonders Lubos Motl, der kurze Zeit später seinen Lehrstuhl an der Harvard University verließ, überschlug sich mit persönlichen Angriffen. Auch andere bekannte Größen der Stringtheorie ließen ihrem Unmut freien Lauf. In Zeitungsartikeln, auf Konferenzen und online feindeten sich beide Seiten an. »Wie viele andere verfolgte ich die Entwicklung wie eine Boulevardzeitung. Es war die Physikversion von Big Brother oder den Kardashians«, resümierte der Physiker Abhishek Agarwal, Redakteur bei der renommierten Fachzeitschrift »Physical Review Letters«.

»Die Diskussion versiegte in den 2010er Jahren schließlich«, sagt Blum. Viele Fachleute waren zuvor davon ausgegangen, dass der 2010 in Betrieb genommene Teilchenbeschleuniger LHC am europäischen Kernforschungszentrum CERN die von der Stringtheorie vorhergesagten Partnerteilchen nachweisen würde. Doch das stellte sich als Irrtum heraus. Bis heute gibt es keinen Hinweis auf eine Supersymmetrie. »Die Stringtheorie ist spektakulär. Viele Stringtheoretiker sind wunderbar. Aber die Erfolgsbilanz für qualitativ korrekte Aussagen über das Universum ist wirklich miserabel«, sagte der Physiker Nima Arkani-Hamed 2024 zu »Quanta Magazine«.

Leider blieben auch andere Hinweise auf eine Physik jenseits des Standardmodells aus. »Dadurch geriet die Grundlagenphysik allgemein unter Druck«, sagt Blum, »nicht nur die Stringtheorie.« Plötzlich spielten die internen Streitigkeiten von Quantengravitationstheoretikern keine so große Rolle mehr, als sich außerdem Physiker aus anderen Gebieten wie der Festkörperphysik über die Vergabe von Forschungsgeldern beschwerten.

Nach der Krise ist vor der Krise

Was hat sich seither im Bereich der Quantengravitation getan? »Noch immer sind die Stringtheorie und die Schleifenquantengravitation die wichtigsten Vertreter, wenn man die Größe der Community betrachtet«, bilanziert Blum. Doch beide Gebiete scheinen seit mehreren Jahren zu stagnieren. »Die vollmundigen Ankündigungen, wie es sie in den 1990er Jahren gab, bleiben inzwischen aus«, erklärt der Wissenschaftshistoriker. Angesichts der Kritik, die es in der Vergangenheit gegeben hatte, lehnen sich die Forschenden nicht mehr so weit aus dem Fenster. »Auch der Wissenschaftsjournalismus ist in den Bereich zurückhaltender geworden«, sagt Blum.

Rollentausch

Seit den so genannten »String wars« haben sich die Gemüter beruhigt, wie eine 2014 stattgefundene Konferenz in Puerto Rico verdeutlicht. Dort wurden Carlo Rovelli, einer der berühmtesten Vertreter der Schleifen-Quantengravitation, und der renommierte Stringtheoretiker Raphael Bousso auf die Bühne geholt und gebeten, jeweils ein Plädoyer für die Gegenseite zu halten. Herauskam eine freundliche und voller Witze und Ironie geführte Debatte, bei der die beiden Physiker auf die Schwächen der jeweiligen Theorien eingingen.

In den vergangenen Jahren hat sich der Fokus vieler Stringtheoretiker verschoben. Statt weiterhin nach einer Weltformel zu suchen, widmen sich viele der Anwendung stringtheoretischer Konzepte auf andere Bereiche wie die Kernphysik oder die Festkörperphysik. Die Grundlage dafür legte eine Entdeckung, die der argentinische Physiker Juan Maldacena im Jahr 1997 machte. Er fand eine Verbindung zwischen einer fünfdimensionalen Raumzeit mit Quantengravitation (einer einfachen Version der Stringtheorie) und einer bestimmten Quantenfeldtheorie ohne Schwerkraft, die sich auf deren vierdimensionalem Rand abspielt. Diese als AdS-CFT-Korrespondenz bekannte Verbindung wird seither intensiv erforscht und lässt sich etwa zur Beschreibung von Phasenübergängen nutzen – für eine Quantengravitationstheorie eignet sie sich hingegen bislang nicht.

Auch die Schleifenquantengravitation scheint festzustecken. Sie liefert keine Vorhersagen, die sich in naher Zukunft überprüfen ließen. Ebenso ist unklar, ob sich die Modelle der Raumzeit, die sich aus der Theorie ergeben, mit den von uns beobachteten Symmetrien decken.

Da die zwei bisherigen Favoriten nicht weiterkommen, wenden sich Fachleute nun vermehrt anderen Herangehensweisen zu. »Mit der Krise der spekulativen Ansätze bekommen bescheidenere Ideen Aufwind«, erklärt Blum. So sei beispielsweise die »asymptotische Sicherheit« ein wachsender Bereich, der ohne zusätzliche Teilchen oder Raumdimensionen auskommt. »Die Hauptschwierigkeit ist bei allen Theorien aber die mathematische Komplexität«, sagt Blum. »Man muss die atomistische Materie mit einer kontinuierlichen Raumzeittheorie verbinden.« Die Stringtheorie tut das, indem sie auf eindimensionale Fäden zurückgreift, die Schleifenquantengravitation hingegen durch eine gekörnte Raumzeit.

Wieder andere, wie der Physiker John Oppenheim, verfolgen einen völlig abweichenden Gedanken. Oppenheim vertritt die unkonventionelle Ansicht, dass die Schwerkraft überhaupt nicht den Gesetzen der Quantenphysik folgt, sondern sich auch weiterhin durch eine klassische Theorie beschreiben lässt. »Im Prinzip folgt er damit dem allgemeinen Trend, einen minimalistischen Ansatz zu wählen«, stellt Blum fest, »nachdem jahrzehntelang ausladende Spekulationen die Nase vorne hatten.«