
aus spektrum.de, 17.12.2023 Schon außerhalb des Schwarzen Lochs tummeln sich extreme und mysteriöse
Phänomene wie Jets und relativistische Scheiben. Doch hinter dem
Ereignishorizont stößt die Physik wirklich an ihre Grenzen. zu Jochen Ebmeiers Realien
»Glaube, nicht Wissenschaft! 60 Jahre ohne einen Beweis, aber sie glauben!« Diese dramatischen Worte wählt der 1934 geborene Mathematiker Roy Kerr in seiner neuesten, noch nicht begutachteten Arbeit. Seine Anschuldigungen betreffen eine Argumentation der beiden renommierten Physiker Stephen Hawking und Sir Roger Penrose: dass im Inneren von Schwarzen Löchern zwangsläufig eine Singularität lauert. Letzteres bedeutet, dass die Schwerkraft unendlich wird. Wie Kerr nun behauptet, sei das keineswegs gesichert – demnach könnten Schwarze Löcher völlig anders aussehen, als die Fachwelt bisher annahm.
Die Singularität ist eine Art physikalische Unmöglichkeit, die sich im Herzen der Schwerkraftmonster verbergen soll: unendliche Dichte, unendliche Schwerkraft, unendliche Raumkrümmung. Bisher gingen Fachleute davon aus, dass eine solche Singularität die Grenzen aufzeigt, an denen eine Theorie gültig ist. Dass aber Einsteins allgemeine Relativitätstheorie solche Unendlichkeiten in Schwarzen Löchern vorhersagt, hatte bisher kaum jemand in Frage gestellt. Bis jetzt.
Auch wenn Kerr Mathematiker ist, ist er im Bereich der Kosmologie kein unbeschriebenes Blatt. Im Gegenteil: Tatsächlich finden sich in dem Fachgebiet einige Größen, die seinen Namen tragen. Denn es war Kerr, dem es erstmals gelang, ein realistisches mathematisches Modell eines Schwarzen Lochs zu entwickeln. Und nun könnte er unsere Anschauung dieser galaktischen Ungetüme auf den Kopf stellen. »Das ist die vielleicht überraschendste Entwicklung in der theoretischen Physik, die ich seit einem Jahrzehnt gesehen habe«, schreibt die theoretische Physikerin Sabine Hossenfelder vom Munich Center for Mathematical Philosophy auf X.
Schwarze Löcher tauchen von Anfang an auf
Modelle von Schwarzen Löchern sind so alt wie die allgemeine Relativitätstheorie selbst. Als Albert Einstein seine Gleichungen im Jahr 1915 veröffentlichte, stürzten sich allerlei Fachleute darauf, um daraus ein Modell unseres Universums herzuleiten. Doch das ist alles andere als einfach. Die einsteinschen Feldgleichungen beschreiben, wie Masse und Energie die Raumzeit krümmen – und umgekehrt: wie die Krümmung der Raumzeit die Bewegung von Masse und Energie beeinflusst. Solche gegenseitigen Abhängigkeiten mathematisch aufzulösen, sind bereits eine Meisterleistung. Wollte man mit der allgemeinen Relativitätstheorie unser gesamtes Universum beschreiben, müsste man jedes noch so winzige Objekt und jeden Lichtstrahl im Kosmos korrekt erfassen und ein unermesslich komplexes Gleichungssystem lösen.
 Gekrümmte Raumzeit | Albert Einsteins
allgemeine Relativitätstheorie entwickelt ein geometrisches Bild der
Gravitation: Masse krümmt die Raumzeit und sorgt so für die bekannten
Kräfte
Gekrümmte Raumzeit | Albert Einsteins
allgemeine Relativitätstheorie entwickelt ein geometrisches Bild der
Gravitation: Masse krümmt die Raumzeit und sorgt so für die bekannten
Kräfte
Doch wie sieht es im Inneren des Schwarzen Lochs aus, wenn man den Ereignishorizont passiert? Angenommen, man nähert sich einem solchen galaktischen Ungetüm mit einer eingeschalteten Taschenlampe. Je näher man darauf zugeht, desto besser lässt sich beobachten, wie die Lichtstrahlen abgelenkt werden – die Schwerkraft ist so enorm, dass sie selbst die Bahn der masselosen Lichtteilchen erkennbar krümmt. Würde es irgendwie gelingen, den Ereignishorizont mit der eingeschalteten Taschenlampe unbeschadet zu passieren, sähe man, dass die Lichtstrahlen nun so stark gekrümmt sind, dass sie das Schwarze Loch kreisförmig umgeben – und schließlich im Gravitationsmittelpunkt versinken. Dieser Punkt, an dem selbst Lichtstrahlen ihr Ende finden, wird als Singularität bezeichnet: Dort ist die Krümmung der Raumzeit gemäß der einsteinschen Gleichungen unendlich groß.
Schwarzschilds Entdeckung war äußerst erstaunlich, aber nicht besonders realistisch. Wenn Materie im Universum kollabiert, etwa in einem sterbenden Stern, dann wird sie einen Drehimpuls besitzen – und damit rotieren. Daher stellte sich die Frage, ob rotierende Materie ebenfalls ein Schwarzes Loch erzeugen kann. Diesen Fall zu untersuchen, stellte sich als extrem kompliziert heraus: Über mehrere Jahrzehnte scheiterten alle Versuche, bis schließlich Kerr im Jahr 1963 eine inzwischen nach ihm benannte Lösung der einsteinschen Feldgleichungen präsentierte.
Tatsächlich
sind rotierende Schwarze Löcher weitaus komplizierter aufgebaut als
ruhende. Zum Beispiel enthalten sie nicht nur einen, sondern gleich zwei
Ereignishorizonte, die das Schwarze Loch wie zwei Schalen umgeben. Für
einen äußeren Beobachter macht das zunächst keinen Unterschied: Man
blickt immer noch auf einen Bereich, der jegliches Licht verschluckt.
Alles, was sich jenseits der Grenzen des äußeren Ereignishorizonts
abspielt, hat keinerlei Einfluss auf die äußere Umgebung des Schwarzen
Lochs.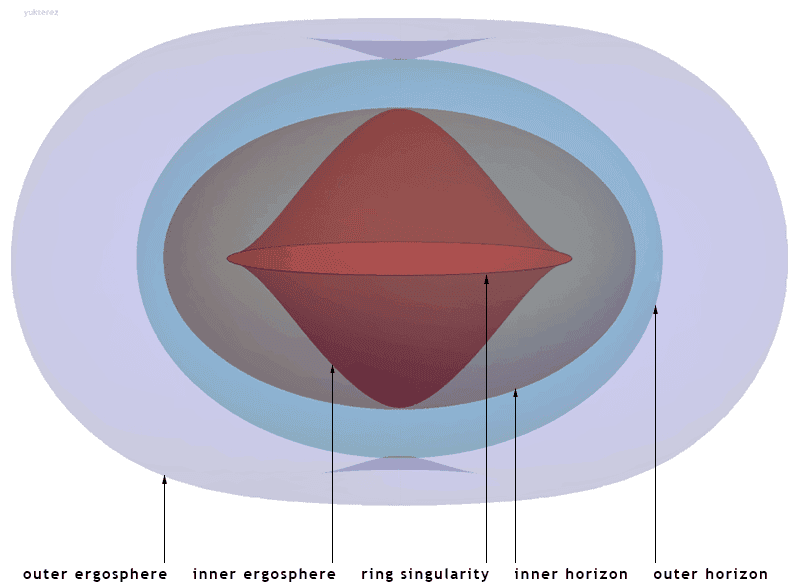 Kerr-Universum | Innerhalb des »inneren
Horizonts« könnten Reisen in die Vergangenheit zumindest theoretisch
möglich sein
Kerr-Universum | Innerhalb des »inneren
Horizonts« könnten Reisen in die Vergangenheit zumindest theoretisch
möglich sein
Da das nicht umsetzbar ist, tasteten sich die Fachleute zunächst langsam
vor. Schon wenige Monate nach Einsteins Veröffentlichung fand der
Astronom Karl Schwarzschild eine erste Lösung der komplizierten
Gleichungen. Dafür betrachtete er eine massive Kugel in einem leeren,
statischen Universum. Trotz der Einfachheit des Modells machte
Schwarzschild eine erstaunliche Entdeckung: Falls die Masse groß ist und
der Radius der Kugel klein, wird die Schwerkraft in der Nähe der Kugel
so stark, dass nicht einmal mehr Licht ihr entweichen kann. Dieser
Grenzabstand, ab dem nicht einmal mehr Licht schnell genug ist, um sich
der Schwerkraft zu entziehen, heißt Ereignishorizont. Dieser umhüllt die
schwere Kugel, so dass man von außen auf völlige Dunkelheit blickt: ein
Schwarzes Loch.
Aber was passiert, wenn man den äußeren Ereignishorizont unbeschadet passiert? Tatsächlich würde man auf ein weiteres Schwarzes Loch blicken! Denn der zweite (»innere«) Ereignishorizont hält alle Materie und alles Licht in seinem Inneren davon ab, nach außen zu dringen (in diesem Fall ist dieses »Außen« aber eben nicht das wirkliche Äußere eines Schwarzen Lochs, sondern der Zwischenbereich zwischen beiden Ereignishorizonten). Würde man weitergehen und in den inneren Ereignishorizont eindringen, fände man keine punktförmige Singularität vor, wo die Krümmung des Raums unendlich wird – sondern eine ringförmige.
Diese beiden Spezialfälle rotierender und nicht rotierender Schwarzer Löcher besitzen also zweifelsfrei Singularitäten. Schon früh stellte sich daher die Frage, ob unendliche Raumzeitkrümmungen notwendigerweise innerhalb aller Schwarzen Löcher entstehen. 1972 behauptete Hawking, aufbauend auf eine Arbeit seines Kollegen Penrose, dass dies der Fall sei. Seither ist es zu einer Art Mantra der Kosmologie geworden: Schwarze Löcher bergen in ihrem Innern Singularitäten.
Von endlichen Kurven zu Unendlichkeiten
Doch wie beurteilt man überhaupt, ob hinter einem Ereignishorizont eine unendliche Raumzeitkrümmung existiert? In der Tat war das Argument von Hawking und Penrose ein mathematisches, sie betrachteten die Eigenschaften von Kurven. Die Idee ist folgende: Angenommen, eine Murmel bewegt sich durch die leere Raumzeit. Sie wird sich für immer und alle Zeit weiterbewegen und niemals anhalten.
Auch in einer nicht leeren Raumzeit kann man untersuchen, wie lange die Murmel ihrer natürlich komplizierteren Flugbahn folgt. Manche Murmeln fliegen hier ebenfalls unendlich weiter. Doch theoretisch kann eine Kugel eine endliche »Lebenszeit« besitzen – und irgendwann plötzlich aus dem Universum verschwinden. Das geht nur, wenn es eine Singularität in der Raumzeit gibt. Könnte man also nachweisen, dass es innerhalb von Schwarzen Löchern Flugbahnen mit begrenzten Lebenszeiten gibt, so die Überlegung von Hawking und Penrose, dann bergen die galaktischen Objekte in ihrem Inneren Singularitäten. Bis hierhin stimmt ihnen Kerr zu.
Aber natürlich haben Hawking und Penrose ihre Argumentation nicht auf eine Murmel gestützt, sondern mit abstrakten mathematischen Objekten gearbeitet. Sie betrachteten Kurven, die dem Verlauf von Lichtstrahlen entsprechen. Falls die Kurven eine endliche »Lebenszeit« besitzen, so die Idee, dann müssten die Strahlen zwangsweise in einer Singularität enden.
Das klingt zwar schlüssig, doch der Übergang von einer langsamen Murmel zu Lichtstrahlen, die sich mit Lichtgeschwindigkeit ausbreiten, bringt Schwierigkeiten mit sich. Gemäß der Relativitätstheorie gilt nämlich: Je schneller sich ein Objekt bewegt, desto langsamer vergeht für dieses die Zeit (im Vergleich zu ruhenden Beobachtern). Bei Licht bleibt die Zeit sogar ganz stehen. Sprich: Licht altert nicht. Somit ist es nicht möglich, die »Lebenszeit« eines Lichtstrahls zu bestimmen. Diese wäre immer null – egal ob ein Lichtstrahl in einer Singularität endet oder sich unbegrenzt fortsetzt.
Deshalb behalfen sich Penrose und Hawking mit einer anderen mathematischen Größe, die der Lebenszeit einer Kurve ähnelt: der so genannten affinen Länge. Das erschien naheliegend, denn alle Objekte, die sich langsamer als das Licht bewegen und eine endliche Lebenszeit besitzen, haben auch eine endliche affine Länge – und umgekehrt. Und das Gute: Auch Lichtstrahlen kann man affine Längen zuordnen, die sowohl endlich als auch unendlich ausfallen können.
»Das ist nichts als ein Dogma« Roy Kerr, Mathematiker
Penrose konnte 1965 zeigen, dass innerhalb eines abgeschlossenen Ereignishorizonts, wie er in Schwarzen Löchern vorkommt, immer Lichtstrahlen mit endlicher affiner Länge existieren. Zusammen mit Hawking argumentierte er: Falls Lichtstrahlen mit endlicher affiner Länge existieren, dann müssen sie in einer Singularität enden. Verbindet man diese beiden Erkenntnisse, dann folgt daraus, dass jedes Schwarze Loch zwangsläufig eine Singularität birgt.
Doch das hat Kerr nun widerlegt. »Der Grund, warum fast alle Fachleute glauben, dass lichtartige Kurven mit endlicher affiner Länge zwangsläufig in Singularitäten enden, ist nichts als ein Dogma«, schreibt der Physiker in seiner aktuellen Veröffentlichung. Auch wenn Penrose einen stichhaltigen Beweis für die Existenz von Lichtstrahlen endlicher affiner Länge innerhalb von Ereignishorizonten vorgebracht hat, ist der zweite Teil der Argumentation unbewiesen: Es gibt keinen stichhaltigen Beweis dafür, dass Lichtstrahlen mit endlicher affiner Länge zwangsläufig in einer Singularität enden. Und tatsächlich konnte Kerr nun zeigen, dass diese Annahme falsch ist.
»Zur Schande vieler theoretischer Physiker – mich eingeschlossen – ist Kerrs Argumentation nicht einmal besonders kompliziert« Sabine Hossenfelder, Physikerin
Kerr hat in seiner Arbeit Lichtstrahlen endlicher affiner Länge innerhalb eines Schwarzen Lochs konstruiert, die keinen Endpunkt besitzen. Sie laufen unendlich lange weiter – und enden damit nicht in einer Singularität. Das zeigt, dass sich die affine Länge für Lichtstrahlen von der Auffassung einer Lebenszeit langsamer Objekte unterscheidet. »Kerrs Berechnung scheint aus mathematischer Sicht korrekt zu sein«, sagt die Physikerin Hossenfelder in einem Video. »Zur Schande vieler theoretischer Physiker – mich eingeschlossen – ist Kerrs Argumentation nicht einmal besonders kompliziert.«
»Wenn die Theorie Singularitäten vorhersagt, ist die Theorie falsch!«Roy Kerr, Mathematiker
Mit seinem Ergebnis hat Kerr allerdings nicht bewiesen, dass Schwarze Löcher ohne Singularitäten existieren. Er hat lediglich gezeigt, dass die Argumentation, auf die sich Fachleute bislang stützten, falsch ist. »Nur weil der Beweis einen Fehler enthält, heißt das nicht, dass die Folgerung daraus falsch ist«, sagt Hossenfelder.
Zudem glauben die meisten Fachleute ohnehin nicht, dass die allgemeine Relativitätstheorie allein geeignet ist, um die Phänomene innerhalb Schwarzer Löcher zu beschreiben. Dort ist die Materie so stark komprimiert, dass ebenso quantenphysikalische Kräfte eine Rolle spielen. Um die dortigen Geschehnisse zu erklären, braucht man vermutlich eine vereinigte Theorie, die alle vier Grundkräfte umfasst. Dem stimmt auch Kerr zu. In seiner Veröffentlichung schreibt er: »Ich bezweifle nicht und habe auch nie daran gezweifelt, dass die Verschmelzung von Relativitätstheorie und Quantenmechanik zeigen wird, dass es nirgendwo Singularitäten gibt. Wenn die Theorie Singularitäten vorhersagt, ist die Theorie falsch!«
Nota. - Kerr tut beiläufig auch dem gesunden Menschenverstand einen Gefallen. Daran, dass wir uns den Begriff des Unendlichen immer wieder mal denken müssen, hat uns Einstein gewöhnt. Die Idee der Singularität mutet uns aber zu, uns das Unendliche - un-endlich Kleine, unendlich Große - wahr und wahrhaftig auch vorzustellen. Diese Verren-kung erspart uns Kerr. Spricht das für oder gegen ihn?
JE


Keine Kommentare:
Kommentar veröffentlichen