Schönheit ist die Teilhabe der Dinge am Ganzen.

griechisch, geometrische Periode             aus Über Ästhetik, Rohentwurf, 19.

 
Schönheit wäre, nach Plotin-Platon, die Teilhabe der Dinge am All-Einen, méthexis; Grade der Schönheit = Grade der Teilhabe. Renaissance (Marsilio Ficino; Leone Eb-reo); Klassik!

Ein Ding ästhetisch betrachten: es so betrachten, daß hinter seiner so-und-so-Be-stimmtheit sein 'Anteil' an der unendlich-zu-bestimmenden-Unbestimmtheit er-sichtlich wird; immerhin für die, die sehen können. Daher der Appell-Charakter des Schönen (vgl. Ficino: kálos von káleo, ich rufe an): es fordert zu (weiterem, aber endlosen) Bestimmen heraus. - Und das nennt man poetisch. 

Moderne, Romantik: Eine Zeit, die sich das All-Eine nicht länger als heil (=harmo-nisch) vorstellen kann, sondern nur noch zerrissen, als sinnloses, disparates Chaos, wird die 'Teilhabe' der Dinge daran nicht länger schön nennen wollen! Und eben diese Sicht der Dinge und der Welt wird von nun an „die ästhetische“ (die poeti-sche) sein.


Nota. - Für Odo Marquard stellt - im Gefolge von Joachim Ritter - das machtvolle Aufkommen des Ästhetischen in der Neuzeit eine Kompensation dar für die verlo-rene Teilhabe am Ganzen, den die Säkularisierung mit sich gebracht habe. Das hätte Sinn, wenn das Ästhetische positiv als eine Füllung und Erfüllung aufgefasst wer-den könnte: Teilhabe am kosmischen Einklang. Das Schöne trägt aber seit seinem Neuauftritt in der Renaissance zunehmend das Signet des ewig Unerfüllten, des Mangels an sich: Eros strebt nach dem Schönen, weil er es nicht hat. Teilhabe an universeller Disharmonie: Es wird immer mehr zu einem Lösungsmittel, das den Verlust des Ganzen reizvoll scheinen lässt. - Kunst entzweit den Menschen, sagt Schiller.
25. 2. 15

 

 

Wie Vernunft und Wahrheit zusammenhängen.

                                          aus Philosophierungen

Dass sich ohne die Prämisse, dass Wahrheit sei, nichts Vernünftiges denken lässt, bedeutet noch nicht, dass es sie wirklich gibt.
8. 2. 14 

Unter Vernunft verstehen wir ein Denken unter der Prämisse, dass Vernunft sein soll. Die Voraussetzung, auf der sie beruht, kann die Vernunft nicht rückwirkend beweisen. Sie setzt gewissermaßen "sich selbst voraus". Sie ist mehr als ein Postulat; sie ist Projekt und muss sich praktisch bewähren. 

Sie können es selbst versuchen: Eine andere Erklärung dessen, was Vernunft sei, werden Sie nicht zustande bringen.
28. 3. 20

 

Nota. Das obige Foto gehört mir nicht, ich habe es im Internet gefunden. Wenn Sie der Eigentümer sind und seine Verwendung an dieser Stelle nicht wünschen, bitte ich um Nachricht auf diesem Blog. JE

Brunelleschis Perspektive.

 
aus spektrum.de, 27.12.2024                                                 zu Geschmackssachen zu Jochen Ebmeiers Realien

Eine neue Art der Geometrie dank dem Dom zu Florenz

Manchmal braucht es Tatendrang: Der ambitionierte Bau eines Doms verleitete Filippo Brunelleschi dazu, Zeichnungen etwas mathematischer zu gestalten – was schließlich zur projektiven Geometrie führte.

von Manon Bischoff

Viele Menschen denken, Mathematik sei kompliziert und öde. In dieser Serie möchten wir das widerlegen – und stellen unsere liebsten Gegenbeispiele vor: von schlechtem Wetter über magische Verdopplungen hin zu Steuertricks. Die Artikel können Sie hier lesen oder als Buch kaufen.

Es gibt eine Sache in der Mathematik, die mich regelmäßig verwirrt. Immer wieder veröffentlichen Forschende Arbeiten mit neuen Erkenntnissen, die allerdings darauf aufbauen, dass die riemannsche Vermutung richtig ist. Sprich, die Fachleute nutzen die Vermutung bei dem Beweis eines anderen Ergebnisses. Das Problem: Niemand weiß, ob die riemannsche Vermutung wirklich korrekt ist. Seit mehr als 160 Jahren versuchen Mathematiker sie zu beweisen – oder zu widerlegen. Erfolglos.

In einer Vorbesprechung zum Podcast »Geschichten aus der Mathematik« habe ich mit meinem Kollegen Demian Nahuel Goos über dieses Phänomen geredet. »Das ist doch total verrückt«, meinte ich damals. »Das ist ja, wie wenn man anfangen würde, ein Haus zu bauen, ohne zu wissen, ob es überhaupt Balken gibt, die stark genug sind, um es zu stützen.« Demian lachte damals und erzählte mir die Geschichte vom Bau des Doms in Florenz, Santa Maria del Fiore. Dort war genau das der Fall.

Der Dom sollte ein besonders imposantes Bauwerk werden und Florenz damit andere Städte wie Venedig oder Pisa übertrumpfen. Hauptattraktion sollte eine riesige Kuppel sein. Der Dom wurde im 15. Jahrhundert quasi fertig gestellt. »Quasi«, weil im Kirchenbau noch ein riesiges Loch klaffte. Von der Kuppel fehlte jede Spur. Denn: Niemand wusste, wie man so eine gigantische Dachkonstruktion bewerkstelligen sollte. So wie die heutigen Mathematiker auf die riemannsche Vermutung setzen, hatten auch die Bauherren im Mittelalter in der Hoffnung begonnen, dass im Lauf der Zeit eine clevere Lösung gefunden werden würde.

Und tatsächlich gab es eine Person, die sich der Herausforderung stellte und mit Kreativität und Einfallsreichtum gesegnet war: Filippo Brunelleschi (1377–1446) – der noch nicht einmal gelernter Architekt war, sondern Goldschmied. Der begnadete Handwerker entwarf nicht nur eine Kuppel, die noch größer war als die ursprünglich geplante, sondern legte auch den Grundstein für eine neue Form der Geometrie, indem er seinen Zeichnungen Tiefe verlieh.

Bilder neu gedacht

Seit Jahrtausenden beschäftigt sich die Menschheit mit Geometrie. Eines der bedeutendsten Werke in diesem Gebiet, »Elemente«, stammt von dem antiken griechischen Gelehrten Euklid, der im 3. Jahrhundert vor unserer Zeitrechnung lebte. Darin formulierte er das Grundgerüst der Geometrie

Anhand möglichst weniger, dafür eingängiger Grundannahmen wollte er Schritt für Schritt alle Prinzipien des mathematischen Bereichs ableiten. Und tatsächlich sind es immer noch seine fünf Regeln, die wir wahrscheinlich im Kopf haben, wenn wir das Wort Geometrie hören. Denn genau diese Regeln werden im Schulunterricht gelehrt.

1. Postulat: Durch zwei Punkte in der Ebene lässt sich exakt eine Linie ziehen.
2. Postulat: Eine Linie zwischen zwei Punkten lässt sich beliebig verlängern.
3. Postulat: Es ist stets möglich, aus einem Punkt und einem vorgegebenen Radius einen Kreis zu zeichnen.
4. Postulat: Alle rechten Winkel stimmen überein.
5. Postulat: Zu jeder Geraden gibt es eine einzige Parallele mit festem Abstand.

All das wusste Brunelleschi wahrscheinlich, so wie seine Zeitgenossen. Aber diese Art der Geometrie fängt nicht ein, wie wir die Welt sehen. Objekte scheinen mit zunehmender Entfernung zu uns zu schrumpfen. Das zeigt sich auch an Bahngleisen, die einen festen Abstand zueinander haben. Dieser wirkt mit wachsender Distanz immer kleiner, und es scheint so, als würden sich die Gleise am Horizont treffen.


Perspektive | Parallele Geraden treffen sich im Fluchtpunkt – das ist einer der zentralen Unterschiede zwischen der euklidischen und der projektiven Geometrie.

Genau diese Effekte wollte Brunelleschi in seinen Zeichnungen einfangen, um sie realistischer erscheinen zu lassen. Und zwar nicht so wie einige seiner Zeitgenossen in ihren Gemälden irgendwie nach Gefühl (weshalb manche Bilder aus der Zeit völlig falsche Größenverhältnisse aufweisen), sondern mit der nötigen mathematischen Stringenz. Die Mathematik hatte dem Architekten schon den Bau der beeindruckenden Kuppel in Florenz ermöglicht. Nun sollte das Fach ihm dabei helfen, die dreidimensionale Welt möglichst exakt in einem zweidimensionalen Bild darzustellen.

Brunelleschi ging sogar so weit, dass er eines seiner Bilder vor einer Szene platzierte, die er gezeichnet hatte, es herumdrehte und ein winziges Loch hineinschnitt. Dann bat er Menschen, von der Rückseite des Bilds durch das Loch auf die Szene zu blicken. Anschließend nahm er einen Spiegel und führte ihn vor das Bild, damit er seine Zeichnung reflektierte. Die Person, die immer noch durch das Loch sah, konnte dadurch erkennen, wie realistisch Brunelleschis Darstellung war.

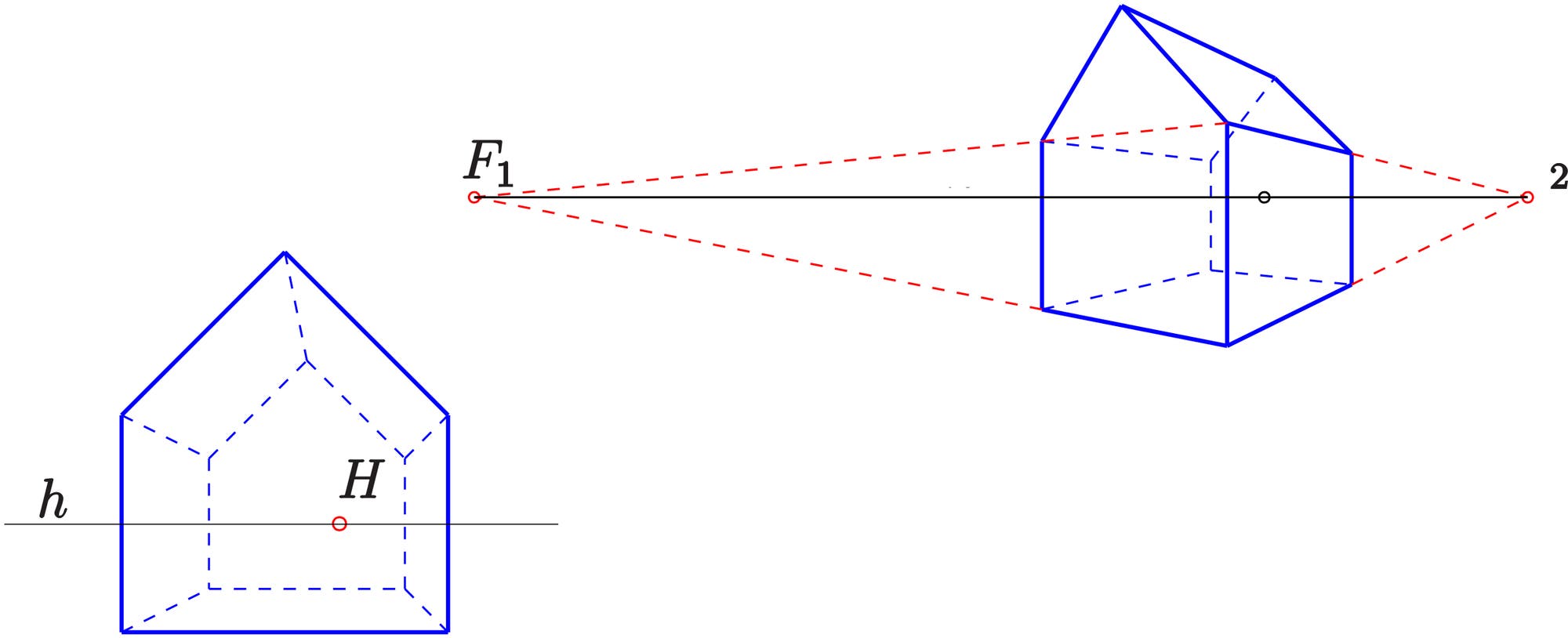Fluchtpunkte | Möchte man ein Haus perspektivisch zeichnen, kann man einen oder mehrere Fluchtpunkte festlegen. 

Damit begründete Brunelleschi die darstellende Geometrie, die einige von Ihnen vielleicht aus dem Kunstunterricht kennen. Dort wählt man zum Beispiel einen oder mehrere Fluchtpunkte, in denen alle Geraden, die in der dreidimensionalen Welt parallel sind, zusammenlaufen. Damit verleiht man den dargestellten Objekten die korrekten Proportionen und Öffnungswinkel: So als hätte das Bild wirklich Tiefe. Richtig angewendet, lassen sich aus einer perspektivischen Zeichnung die tatsächlichen Größen von Objekten ableiten, sofern man einen Maßstab besitzt.

Ein mathematisches Grundgerüst

Die Kunstszene zeigte sich schnell beeindruckt von den neuen Techniken. Infolgedessen übernahmen einige Künstler die neuen Methoden und verfeinerten sie. Für die Mathematik war diese Entwicklung anfangs uninteressant – schließlich ist in unserer dreidimensionalen Welt Euklids Geometrie realisiert. Die perspektivischen Ansätze von Brunelleschi waren nur ein Hilfsmittel, um das Dreidimensionale realistisch in einer Ebene einzufangen.

Nicht nur Brunelleschis Kollegen erfreuten sich an den neuen Methoden, sondern auch er selbst. Er berücksichtigte die mathematischen Erkenntnisse über seine Zeichnungen hinaus in seiner Architektur. Er hat seine Bauten so konzipiert, dass sie perspektivisch harmonisch sind, etwa durch ganzzahlige Proportionsbeziehungen. Das sieht man besonders gut in der Basilica di San Lorenzo, einer weiteren Kirche in Florenz, die als »Kirche der Medici« bekannt ist.

Zwischen dem 17. und 18. Jahrhundert erkannten Mathematiker, dass das perspektivische Zeichnen festen Regeln folgt, die sich durch die Sprache der Mathematik einfangen lassen. Sie fingen deshalb an, ein neues Regelwerk für diese Art der Geometrie aufzustellen – denn offensichtlich gelten dort nicht mehr alle altbekannten Postulate von Euklid. Zum Beispiel stellen die Fluchtpunkte so etwas wie einen unendlich fernen Punkt dar: der, in dem selbst parallele Geraden sich treffen. Für eine solche Situation stringente mathematische Regeln aufzustellen, erwies sich als extrem komplexe Aufgabe. Deshalb wurde erst in der ersten Hälfte des 19. Jahrhunderts die so genannte projektive Geometrie begründet.

Um eine realistische Zeichnung anzufertigen, muss man nicht unbedingt Experte in der projektiven Geometrie sein. Da genügt es durchaus, die Regeln der Perspektive zu kennen, die Brunelleschi aufgestellt hat. Doch Kunst entwickelt sich ja weiter – inzwischen kommen in dem Bereich immer öfter Computer zum Einsatz. Und damit sie eine Szene wahrheitsgetreu darstellen, brauchen sie feste mathematische Anweisungen. In diesem Fall bieten sich die Methoden der projektiven Geometrie an. Die kommt ebenfalls bei Computerspielen zum Einsatz. Auch diese erzeugen zweidimensionale Bilder auf einem Bildschirm, die einer dreidimensionalen Welt ähneln sollen – so wie bei Brunelleschis Zeichnungen.

Eine große Herausforderung im Bereich der Informatik ist es aktuell, KI-Programmen ein solches geometrisches Verständnis beizubringen, damit sie ein räumliches Verständnis entwickeln. So sollen künftige Algorithmen aus zweidimensionalen Aufnahmen ableiten können, was sich in der dreidimensionalen Welt abgespielt hat. Mal schauen, wann sie Brunelleschis Methoden verinnerlicht haben.

Woke hat das freiheitliche Prinzip zum Gespött gemacht.

Ducreux et al.

Es wird Zeit, dass es den Knüppel aus dem Sack holt..

Jagen – der männliche Anteil am spezifisch Menschlichen.

                                         aus Männlich                                       
Der Mensch ist das einzige Tier, das aufrecht geht.

Das einzige Tier, das Städte baut.

Das einzige Tier, das nach seinem Dasein fragt…

Und Homo sapiens ist einzige Spezies, wo der männliche Teil der Population eine eigene, geschlechtsspezifische Rolle in der Reproduktionsweise der Gattung spielt.







Nämlich als Jäger.




Auch unsere nächsten Verwandten, Schimpansen und Bonobos, jagen. Aber nur ge-legentlich, wenn die Situation sich ergibt. Zu selten, als dass sich daraus innerhalb der gemeinsam jagenden Gruppe eine fortwährende Arbeitsteilung ausbilden könn-te. Und zu unregelmäßig, als dass sich die individuell unterschiedlichen Jagdfertig-keiten auf die Rangordnung innerhalb der Gruppe auswirken würden. Es ist ein okkasionelles Beiwerk zum vorherrschenden Aufsammeln von Nahrung.

Erst Homo habilis jagt regelmäßig. Die Jagd in der offenen Savanne unterscheidet sich qualitativ von der Jagd auf kleinere Tiere im Urwald. Denn hier trifft der Mensch auf Nahrungskonkurrenten, die stärker sind als er. Das gilt schon und so-gar besonders für die Anfangszeit, wo der Mensch noch nicht selber Beute reißt, sondern erst an der verlassenen Rissen der Großkatzen mitzehrt; denn hier trifft er außer auf die Katzen auch auf einen besonders gefährlichen Konkurrenten – die im Sozialverband jagenden* Hyänen. Die Verteidigung gegen die Rivalen im offenen Feld erfordert Organisation. Kooperation wird regulär; während das Sammeln der Frauen im Umreis des Lagers individuell und unkoordiniert geschehen kann.

Dem Menschen ist das Jagen im Verbund nicht, wie Hyänen und weiblichen Lö-wen, genetisch angestammt. Es war eine gattungsgeschichtliche Neuerwerbung. Das fehlende genetische Programm musste durch ein allgegenwärtiges Medium der Ver-ständigung ersetzt werden. Die Entwicklung eines dauerhaften Systems von Laut-symbolen war eine Voraussetzung für die Habitualisierung der Jagd.

Auf der andern Seite ermöglichte erst die erhebliche Steigerung der Eiweißaufnah-me, die durch Fleischkost möglich wurde, jene Vergrößerung der Hirnmasse in der Familie Homo, die ihrerseits die Voraussetzung für die Entwicklung der Sprache war, die uns zu sapientes macht.

Ohne das Jagen wären wir nicht zu Menschen geworden. Ohne die Jäger kein Sapiens.

 
*) Es ist ein Irrtum, dass Hyänen feige wären und sich nur von Aas ernährten. Sie sind kühne und gefährliche Jäger.

23. 1. 15 

 

 

 

Intelligenz und/oder Kommunikation.

aus spektrum.de, 23.12.2024                                                                          zu Jochen Ebmeiers Realien

Soziale Kognition
Ameisen profitieren von Teamarbeit mehr als Menschen
Manche Probleme lassen sich in der Gruppe besser lösen als allein, etwa sperrige Gegenstände durch enge Öffnungen zu manövrieren. Ameisen stellen sich bei solchen Aufgaben umso geschickter an, je mehr Helfer sie haben – anders als Menschen

von Anna von Hopffgarten

Ameisen verfügen über eine ausgeprägte soziale Kognition – viele Aufgaben erledigen sie in der Gruppe. In bestimmten Bereichen kann ihre Teamfähigkeit sogar jene von Menschen übertreffen, wie eine Arbeitsgruppe um Ofer Feinerman vom Weizmann Institute of Science im israelischen Rehovot herausgefunden hat.

Die Fachleute ließen jeweils verschieden große Gruppen von Menschen und von Ameisen der Art Paratrechina longicornis einen T-förmigen Gegenstand durch zwei hintereinanderliegende Türen manövrieren. Die Form des Objekts und die Geometrie der Räume stimmte bei allen Teams überein, nur die Größe variierte entsprechend der Zahl der Mitstreiter und der Körpermaße. Bei den Ameisen war der Gegenstand zudem vorher in Katzenfutter gelagert und mit Thunfisch eingerieben worden, um die Tiere dazu zu motivieren, ihn durch die beiden Öffnungen zum Nest zu transportieren.

Die Ameisen mussten die Aufgabe entweder allein erledigen oder in Gruppen von 7 oder 80 Tieren. Die menschlichen Probandinnen und Probanden waren in Einzelpersonen, sechs bis neun Personen starke Teams oder in Gruppen mit 16 bis 26 Teilnehmern aufgeteilt. Von den Menschenteams wiederum erhielt die Hälfte die Anweisung, weder zu sprechen noch zu gestikulieren. Sie trugen zudem Masken und Sonnenbrillen, damit ihre Kommunikationsmöglichkeiten jenen der Ameisen ähnelten. 

Das »Klavierträgerproblem« | Eine Gruppe von Ameisen (oben) und eine Gruppe von Menschen (unten) manövrieren jeweils ein T-förmiges Objekt durch zwei aufeinander folgende Türen

Kleines Gehirn macht soziale Kognition bedeutsamer

Die Fachleute verfolgten die Bewegung der Last und analysierten den zurückgelegten Weg und die Erfolgsquote. Dabei stellten sie fest, dass große Ameisengruppen deutlich besser abschnitten als einzelne Tiere oder kleine Gruppen. Bei den in ihrer Kommunikation eingeschränkten Menschen dagegen stellten viele Mitstreiter keinen Vorteil dar, im Gegenteil: Große Gruppen lösten die Aufgabe schlechter als Einzelpersonen. Sobald die Teilnehmer miteinander sprechen durften, stieg ihre Leistung allerdings stark an. Eine einzelne Person schnitt zudem immer besser ab als eine einzelne Ameise. Große Ameisengruppen übertrafen aber teils sogar die menschlichen Teilnehmer.

Feinerman und seine Kolleginnen und Kollegen schließen daraus, dass ein kleines Gehirn wie das von Ameisen deutlich stärker auf Kooperation angewiesen ist als das komplexe Menschenhirn. Deshalb hätten die Tiere eine besonders effiziente soziale Kognition entwickelt. Menschen dagegen können dank ihres hoch entwickelten Nervensystems viele Aufgaben allein bewältigen. Um erfolgreich mit anderen zu kooperieren, benötigen sie allerdings eine ausgefeilte Kommunikation. 

Nota. - Adorno hat sich abschätzig über die Karriere des Kommunikations-Begriffs geäußert. Es ist ja auch offenbar: Wo immer nur 1+1+1+1+1... addiert würde, wäre ein logischer Aufstieg gar nicht denkbar; es würde Alles immer mehr - aber wann auch besser?   

Und psycho logisch geht bei jedem Kommunikationsschritt ein bissel content ver-loren. 

Mit dem Einbruch des Internet wurde die Mystifikation bis ins Okkulte getrieben: Schwarmintelligenz wurde zu einem Parteiprogramm.

Gewiss sind Intelligenz und Kommunikation keine Antagonisten. Aber einfach komplementär sind sie anscheinend auch nicht. Vielmehr bleibt bloße Kommuni-kation stets auf Ameisenniveau, doch wo immer eine Steigerung erforderlich wird, muss Intelligenz... dazukommen? Nein: drüber hinaus gehen.
JE

Oh!

Dortmund-„Tatort“ zu Weihnachten

Tagesspiegel, 26. 12. 2024

 

Grau.

Es braucht.

Oberallgäu                                                   zu öffentliche Angelegenheiten

Gestern schrieb ich: Regionale Mundarten pflegen ist löblich - nämlich die eigene. Doch wenn jede*r überall egal schwätzet, hören sie auf, regionale Mundarten zu sein.

Als Edmund Stoiber während des Bundestagswahlkampfs 2002 sagte, "wir müssen den Kindern wieder richtiges Deutsch lernen", erntete er nördlich des Mains viel Heiterkeit; dort wusste man nicht, dass das auf Bairisch richtig ist.

*

Im Norden sagt man: es ist nötig, und hierzu oder dazu braucht man..., und danach kommt eine Erläuterung: wer es braucht und wozu.

Auf Bairisch kann "es braucht" ganz alleine stehen.

In den Siebzigern haben wir gelernt, alles auf die darin versteckten Interessen zu durchleuchten. Doch seit geraumer Zeit heißt es auch im Norden allenthaben: Es braucht!

Das ist nun nicht bloß eitel, wie jeder Gebrauch einer regionalen Mundart in parti-bus, sondern berechnend und hinterhältig: Wer was braucht und wozu soll nicht ans Licht.

Die Bayern sollten das nicht länger tatenlos anhören.

An Weihnachten.

wo?

An Weihnachten, an Ostern, an Himmelfahrt - so liest man's inzwischen in allen Blätter, egal ob in Hamburg, München oder Berlin. Nördlich des Mains sagte man früher zu.

Regionale Mundarten pflegen ist löblich - nämlich die eigene. Doch wenn jede*r überall egal schwätzet, hören sie auf, regionale Mundarten zu sein.

Dann halt lieber Denglish. 

 

 

Gibt es ein Jungenproblem?

                                                              zu Levana, oder Erziehlehre zu Männlich; zu öffentliche Angelegenheiten

In den letzten Jahrzehnten wurde deutlich, dass Mädchen in der Schule besser zurechtkommen als Jungen. Das liegt allerdings nicht an den Jungen und Mädchen, sondern an der Schule. 

 

• Hier eine Dokumentation:

 

Gegen die Verharmlosung von Bildungsmisserfolgen von Jungen

Ergänzungen, Erörterung, Analyse und Hintergründe zur Stellungnahme des Bundesjugendkuratoriums:

„Schlaue Mädchen – Dumme Jungen? Gegen Verkürzungen im aktuellen Geschlechterdiskurs“ vom September 2009

von
MANNdat e.V. – Geschlechterpolitische Initiative - Gemeinnütziger Verein
info@manndat.de
http://www.manndat.de
Postfach 60 14 05,
22214 Hamburg
 
April 2010

Warum diese Stellungnahme? 

 

Das Bundesjugendkuratorium hat im September 2009 eine offizielle Stellungnahme „Schlaue Mädchen – Dumme Jungen? Gegen Verkürzungen im aktuellen Geschlechterdiskurs“ zu den Ergebnissen von Fachleuten veröffentlicht, die einhellig eine problematische Bildungs- und Arbeitsmarktsituation von Jungen konstatieren. Das Bundesjugendkuratorium hat wesentlichen Einfluss auf die Bildungs- und Jugendpolitik, da es die zuständigen Ministerien berät. Die Stellungnahme des Bundesjugendkuratoriums ist deshalb eine sehr wichtige Aussage der Bildungs- und Jugendpolitik in Deutschland. Sie gibt damit einen Trend der Bildungs- und Jugendpolitik auf Bundesebene in den nächsten Jahren, wenn nicht sogar Jahrzehnten, wieder. Grund genug also für MANNdat, diese Stellungnahme des Bundesjugendkuratoriums unter die Lupe zu nehmen.

Zusammenfassung

In Deutschland ist Bildung einer der wichtigsten volkswirtschaftlichen Faktoren. Aber obwohl jeder zehnte Junge ohne Migrationshintergrund und fast jeder vierte Junge mit Migrationshintergrund die Schule ohne einen Abschluss verlässt, ist das Thema Bildungsförderung von Jungen in den Bildungsministerien in Deutschland nicht vollständig angekommen.

Das Bundesjugendkuratorium berät die Bundespolitik in jugendpolitischen Fragen und ist damit mitverantwortlich für die derzeitige geschlechterspezifische Bildungssituation. Die vom Bundesjugendkuratorium verfasste Stellungnahme zur Bildungssituation von Jungen im September 2009 „Schlaue Mädchen – Dumme Jungen? Gegen Verkürzungen im aktuellen Geschlechterdiskurs“ ist keine objektive Abwägung verschiedener Ansätze zur Jungenförderung. Sie stellt vielmehr eine subjektive Verteidigung einseitig sozialisationstheoretischer und männlichkeitskritischer Ansätze dar. Die von unabhängigen Einrichtungen erzielten dramatischen Ergebnisse zur Bildungssituation von Jungen werden relativiert.

Bedürfnisorientierte und motivationale Ansätze zur Jungenförderung bleiben völlig unberücksichtigt. Ein Mangel, der bei der Vielzahl von Fachleuten, die hinter dem Bundesjugendkuratorium stehen, überraschend ist. Eine Förderung von Jungen in den Bereichen, in denen sie sich – in Schuleingangsuntersuchungen belegt – tendenziell langsamer entwickeln (Sprachfähigkeit, Motorik), wird in der Stellungnahme des Bundesjugendkuratoriums überhaupt nicht diskutiert. Somit bleiben wichtige Ansatzpunkte zur Bildungsförderung von Jungen – Förderung schon im Vorschulbereich in Sprachfähigkeit und Motorik, sowie Lesekompetenz während der Schulzeit und die stärkere Berücksichtigung auch jungentypischer Lebenswelten und Belange in der Schulpädagogik – völlig unbeachtet.

Die Behauptung des Bundesjugendkuratoriums, dass sich die Lesekompetenzunterschiede zwischen Mädchen und Jungen von 2001 zu 2006 halbiert hätten, ist verkürzt dargestellt. Tatsächlich sind die geschlechterspezifischen Lesekompetenzunterschiede bei den 15-Jährigen (vgl. PISA-Studien) in den letzten Jahren gleich geblieben.

Die Vorschläge des Bundesjugendkuratoriums zur „Jungenförderung“ beruhen somit auf unvollständigen Voraussetzungen und sind deshalb äußerst fragwürdig. Viele Vorschläge des Bundesjugendkuratoriums zur Verbesserung der Bildungssituation von Jungen sind zudem nichts Neues. Jungen neue, geschlechteruntypische Berufsfelder vorzustellen, ist z.B. eine Forderung, die schon im Jahr 2001 das „Forum Bildung“ gestellt hat. Die Notwendigkeit von mehr Daten zur Situation männlicher Jugendlicher mit Migrationshintergrund hat MANNdat schon im Jahr 2004 im Rahmen eines Petitionsverfahrens gefordert. Vielmehr scheitert es gerade an den bildungs- und jugendpolitisch Verantwortlichen, dass eben diese Maßnahmen nicht umgesetzt, sondern Jungen aus den entsprechenden Maßnahmen bislang bewusst ausgeschlossen wurden und werden, z.B. aus dem Zukunftstag oder aus Situationsberichten von Jugendlichen mit Migrationshintergrund.

Statt sich diesen Versäumnissen zu stellen, wird die Verantwortung den Jungen selbst zugeschoben und ihnen mangelnde Flexibilität ihres Rollenbildes vorgeworfen. Als Lösung empfiehlt das Bundesjugendkuratorium die Fortführung eines „Gender Mainstreaming“, das sich bei konkreter Betrachtung der gleichnamigen Projekte im mit dem Bundesjugendkuratorium kooperierenden Deutschen Jugendinstitut als Verkürzung der geschlechterspezifischen Bildungsförderung auf Mädchenförderung entpuppt. Denn dort hat Gender Mainstreaming das Ziel, „Strategien, die die Benachteiligung von Mädchen und Frauen in Ausbildung und Erwerbsarbeit überwinden“, zu finden. Von einer Beseitigung von Bildungsnachteilen und Bildungsbenachteiligungen von Jungen ist nicht die Rede. Der Bildungsrückstand von Jungen wird stattdessen von Verantwortlichen des Deutschen Jugendinstituts als „bitter notwendig“ im Sinne der Frauenförderung betrachtet.

Mehr als 30 Jahre lang wurden Mädchen gezielt gefördert, um ihre Bildungserfolge zu verbessern, was durchaus sinnvoll und erfolgreich war. Aber in diesen mehr als 30 Jahren hat man Jungen in der Bildung zurück gelassen. Heute, zehn Jahre nach der ersten PISA-Studie, beschränkt sich die Politik vorrangig darauf, die nunmehr umgekehrt vorhandenen Bildungsmisserfolge von Jungen zu relativieren und zu verharmlosen. Die logische Folge: In Baden-Württemberg z.B. erschöpft sich die aktuelle geschlechterspezifische Förderung in Pädagogischen Hochschulen wie eh und je in Mädchenförderprojekten. Gerade die Bildungssituation von Jungen zeigt damit in aller Deutlichkeit das Versagen von „Gender Mainstreaming“ – nach Ansicht des Bundesjugendkuratoriums die vermeintliche Lösung.

Eine Bildungs- und Jugendpolitik auf Basis der Stellungnahme des Bundesjugendkuratoriums, die – wie seit 30 Jahren unverändert – sich auf eine sanktionierende, männlichkeitskritische Sozialisationsarbeit beschränkt und eine motivationale und bedürfnisorientierte Bildungsförderung von Jungen vernachlässigt, ist nicht geeignet, Jungen aus dem Bildungsabseits zu holen.
 


Die Analyse im Einzelnen

Die Bildungssituation von Jungen

Alle objektiven Studien unabhängiger Fachleute zeigen erhebliche geschlechterspezifische Unterschiede, vorwiegend zuungunsten der Jungen. Der Aktionsrat Bildung[1] widmet sein Jahresgutachten 2009 speziell diesem Thema und stellt fest, dass Disparitäten zum Nachteil von Jungen entstanden sind. Der Bildungsbericht 2008[2] kommt zu dem Ergebnis, dass es neue Problemlagen bei Jungen gibt und das Risiko für Jungen und junge Männer zunimmt, im Bildungssystem zu scheitern. Das Berlin-Institut für Bevölkerung und Entwicklung[3] spricht von einer »Bildungskrise der jungen Männer«. Jungen stellen über 60% der Sonderschüler. Sie haben die signifikant höhere Schulabbrecherquote und die signifikant niedrigere Abiturquote. Der Anteil männlicher Schüler in Gymnasien sank von 56% im Jahr 1970 auf 43% im Jahr 2006.[4] Der Bildungsbericht der Stadt Freiburg spricht sogar von lediglich nur noch 40% Anteil männlicher Schüler mit allgemeiner Hochschulreife.[5]

Heike Diefenbach fasst zusammen:

„Drückt man die Nachteile, die Jungen gegenüber Mädchen bezüglich der erreichten Sekundarschulabschlüsse haben, durch den Relativen Risiko-Index als einem Maß für Über- oder Unterrepräsentation aus, so zeigt sich, dass im Durchschnitt der Schuljahre 1990/1991 bis einschließlich 2005/2006 auf drei Jungen, die die Schule mit der Fach-/Hochschulreife verlassen, vier Mädchen, und auf drei Jungen, die die Schule ohne Abschluss verlassen, zwei Mädchen kommen.

Insgesamt gesehen lassen sich also anhand aller gängigen Maße für Schulerfolg erhebliche Nachteile von Jungen gegenüber Mädchen feststellen. Geschlecht ist somit nach wie vor ein Faktor für Schullaufbahn und Schulerfolg,[6] jedoch mit umgekehrtem Vorzeichen, als dies in den 60er-Jahren der Fall war…Heute sind es Jungen, die auf allen Stufen der Schullaufbahn Nachteile haben.“[7]

Die Stellungnahme des Bundesjugendkuratoriums ist keine objektive Arbeit

Anstatt sich den Ergebnissen unabhängiger Fachleute zu stellen, gab die ehemalige Bundesjugendministerin von der Leyen eine Stellungnahme zu den Ergebnissen beim Bundesjugendkuratorium in Auftrag. Das Bundesjugendkuratorium ist keine von der Bundesjugendpolitik unabhängige Stelle. Die Bundesjugendministerin benennt Mitglieder für das Bundesjugendkuratorium.[8] Zudem wird das Bundesjugendkuratorium vom Bundesjugendministerium gefördert. Im Gegenzug dazu berät das Bundesjugendkuratorium die Bundesregierung in grundsätzlichen Fragen der Jugendhilfe und in Querschnittsfragen der Kinder- und Jugendpolitik.[9]

Mit diesem Hintergrundwissen verwundert es nicht, dass die Stellungnahme des Bundesjugendkuratoriums keine objektive Abwägung verschiedener Ansätze zur Jungenförderung ist, sondern einen einseitig sozialisationstheoretischen und männlichkeitskritischen Ansatz kolportiert. Denn genau dieser Ansatz wird seit Jahren von der Jugendpolitik praktiziert. Auffällig ist, dass Wissenschaftler, die einen bedürfnisorientierten, motivationalen Ansatz der Jungenförderung befürworten, wie sie z.B. im „Handbuch Jungen-Pädagogik“ (Beltz-Verlag) vertreten sind, keine ausreichende Würdigung finden, wie es in einer offenen und vor allem objektiven Debatte zu dem Thema sein müsste. Berücksichtigt man, dass hinter dieser Stellungnahme eine Vielzahl hochdotierter Fachleute aus dem Bereich Pädagogik oder Jugendförderung stehen, muss man diesen Mangel als gravierend bezeichnen.

So kann man den Eindruck gewinnen, die Stellungnahme des Bundesjugendkuratoriums bemüht sich um Rechtfertigung für die Vernachlässigung der Jungenbildungsförderung in den vergangenen Jahrzehnten und eine  Relativierung der zunehmenden Bildungs- und Zukunftsmisserfolge der Jungen. Die Stellungnahme des Bundesjugendkuratoriums ist also weniger eine fachliche, wissenschaftliche Auseinandersetzung mit dem Thema, sondern mehr ein politischer Standpunkt.
 
Allein schon der Titel „Gegen Verkürzungen im aktuellen Geschlechterdiskurs“ stellt den wirklichen Sachverhalt auf den Kopf, da die geschlechtersensible Bildungs- und Jugendpolitik der letzten 30 Jahre eine einzige Verkürzung des Geschlechterdiskurses auf Mädchenförderung und Jungenvernachlässigung darstellt. Das Problem besteht also nicht darin, dass nun der Blick nur auf Jungen gerichtet würde.

„Parteiliche Mädchenarbeit blickt auf eine fast dreißigjährige Tradition zurück. In koedukativen Einrichtungen richteten feministische Mädchenarbeiterinnen Mädchenräume ein, und schufen Öffnungszeiten ausschließlich für Mädchen und junge Frauen in oft speziellen Räumlichkeiten.

In fast allen bundesrepublikanischen Städten gibt es inzwischen Mädchentreffs, Mädchenzentren, Zufluchtshäuser, Wohngruppen und spezielle Mädchenberatungsstellen. Der Frauenbewegung nahe stehende Professorinnen initiierten Mädchenprojekte; Vorlesungen und Seminare mit einem parteilichen Ansatz wurden angeboten und feministische Forschung konnte sich im Wissenschaftsbetrieb etablieren. Eine Fülle von Veröffentlichungen, Studien und Projekten halfen mit, Mädchenarbeit als Standard in der Jugendarbeit durchzusetzen. Mädchenarbeit ist vielfältig ideologisch verortet. Sie reicht von konservativer, Problemgruppen beschreibender Mädchensozialarbeit bis hin zu einem radikal-feministischen Arbeitsansatz.“[10]

Kaum eine Stadt oder eine Gemeinde, die nicht spezielle Frauenbeauftragte oder zumindest Frauennetzwerke und spezielle Frauenförderprogramme anbietet. Im Bund und in fast allen Bundesländern wurden Frauenministerien installiert. Die Geldtöpfe für geschlechtsspezifische Arbeit liegen in den Händen dieser Institutionen. Dass hier kein großes Interesse besteht, Jungenförderung zu betreiben, ist klar.

Es waren Bildungs- und Jugendpolitik, die Jungen von Beginn an aus dem größten geschlechterspezifischen Förderprojekt aller Zeiten, das sich zudem noch „Zukunftstag“ nennt, ausgegrenzt haben und bis heute noch in 13 von 16 Bundesländern ausgrenzen.

Ausgrenzung ist eine Form von Gewalt. Das hat uns nicht zuletzt die Geschlechterpolitik immer wieder klar gemacht. Mit dem Ausschluss von Jungen aus dem Zukunftstag haben Bildungs- und Jungendpolitik Maßstäbe für geschlechtersensible Jugendförderung geschaffen. Was folgte, war eine Vielzahl von geschlechtersensiblen Projekten auf allen politischen Ebenen, deren Hauptmerkmal geschlechterspezifischer Förderung das bloße Weglassen von Jungen war und bis heute noch in weiten Teilen ist.

Tatsächlich überragt die Mädchenförderung die Jungenförderung auch heute noch um ein Vielfaches. Eine Analyse der geschlechterspezifischen Förderprojekte im Landkreis Karlsruhe z.B. ergab 2009 ein Verhältnis von Mädchenförderprojekten zu Jungenförderprojekten von etwa 8 zu 1[11].

Einseitige Förderung am Beispiel Baden-Württemberg

In Baden-Württemberg existieren noch eigenständige Pädagogische Hochschulen. Deshalb ist hier die Analyse geschlechtersensibler Bildungsförderung einfacher. Ein Blick auf die derzeitige geschlechterspezifische Förderung an diesen Hochschulen zeigt folgende aktuelle Mädchenförderprojekte:[12] [13]

a) Pädagogische Hochschule Karlsruhe und Hochschule Karlsruhe: „forsche Schülerinnen forschen“, „GirlsLab“ und Feriencamp „Forschungswerkstatt Bionik“
b) Pädagogische Hochschule Heidelberg: „science-live! Labor“
c) Pädagogische Hochschule Schwäbisch Gmünd: „Mut zum Forschen“
d) Pädagogische Hochschule Freiburg: „girls4science“
e) Universität Stuttgart: „Nassy“ (Gewässerforschung) und „SciPhyra“
f) Pädagogische Hochschule Ludwigsburg und Hochschule Heilbronn: „Girl’s Sense“

Allein die Projekte von d) bis f) erhalten von 2009 bis 2011 staatliche Förderung in Höhe von etwa 1,2 Millionen Euro von Seiten des Landesforschungsministeriums und der Bundesagentur für Arbeit.
Jungenförderprojekte gibt es in den Pädagogischen Hochschulen nicht. Dies zeigt deutlich, dass die Politik durch einseitige Subventionierung die Pädagogischen Hochschulen ganz gezielt auf eine einseitige Förderpolitik ausrichtet. Wohlgemerkt, hier handelt es sich um nagelneue, aktuelle Projekte.

Es hat sich also seit 30 Jahren nichts geändert. Man macht etwas Spezifisches für Mädchen, lässt Jungen einfach weg und meint dann, das Thema „Geschlecht“ abschließend behandelt zu haben.
Geworben wird für diese Mädchenbildungsoffensiven in den Pädagogischen Hochschulen zudem noch mit dem Slogan „Ohne Jungs? …nur für uns“. Hier werden Jungen abwertende Klischees kolportiert, da eine pauschale Benachteiligung von Mädchen durch die bloße Anwesenheit von Jungen unterstellt wird, die nur überwunden werden kann, wenn man Jungen gezielt ausschließt – die gleiche Argumentation wie beim Ausschluss von Jungen aus dem Zukunftstag. Dies ist in hohem Maße Jungen abwertend. Abwertung ist ein hochaggressiver Akt.[14]

Datendefizite über Jungen

Das Bundesjugendkuratorium weist zu Recht darauf hin, dass zu wenige Daten zur Lebenssituation von Jungen mit Migrationshintergrund vorliegen:

„Vielmehr muss man festhalten, dass es kaum weiterführende Erkenntnisse zur Situation männlicher Jugendlicher mit Migrationsgeschichte, ihren Bildungsbiographien und ihren Formen der Lebensgestaltung zur Erklärung ihrer Misserfolge im Bildungssystem gibt.[15]

Das Bundesjugendkuratorium verschweigt allerdings, dass die Jugendpolitik dafür die Verantwortung trägt. Es war nämlich die vom Bundesjugendkuratorium beratene Bundesjugendpolitik, die in den Jahren 2001 – 2004 mit großem Aufwand einen Bericht „Viele Welten leben“ erstellen ließ, der allein die Situation weiblicher Jugendlicher mit Migrationshintergrund betrachtete. Männliche Jugendliche mit Migrationshintergrund, also die Klientel mit den größten Bildungsproblemen in Deutschland, wurden dabei ausgeklammert.[16]
 

Abschluss	Jungen (o.M.)	Mädchen (o.M.)	Jungen (m.M.)	Mädchen (m.M.)
Ohne	10,0%	5,8%	22,6%	15,4%
Hauptschule	27,9%	21,0%	42,6%	40,4%
Realschule	39,8%	43,4%	26,4%	32,1%
Gymnasium	22,3%	29,8%	8,5%	12,1%

o.M. = ohne Migrationshintergrund
m.M. = mit Migrationshintergrund

Quelle: MANNdat: Migrantenjungen und Politik, Dezember 2007

Die Folgen dieser einseitigen Betrachtung waren fatal. Im Nationalen Integrationsplan 2007 wurde im Themenfeld 4.4. „Lebenssituation von Frauen und Mädchen verbessern“ eine Integrationspolitik implementiert, die als geschlechterspezifische Komponente wieder ausschließlich den Blick auf Mädchen und Frauen richtet.[17]

Als MANNdat 2004 eine Petition beim Deutschen Bundestag einreichte, mit der Bitte um eine gleichberechtigte Betrachtung der Situation männlicher Jugendlicher mit Migrationshintergrund, wurde dies vom Petitionsausschuss mit der Begründung abgelehnt, es gäbe ausreichend Daten zu männlichen Jugendlichen mit Migrationshintergrund.[18] Eine Aussage, die sich nachträglich als falsch herausstellte. Die Studie „Bildungsmisserfolge von Jungen“ des Bundesbildungsministeriums aus dem Jahr 2007 belegt, dass ein eklatantes Defizit in der Datenlage männlicher Jugendlicher mit Migrationshintergrund besteht.[19]

Wirft man einen Blick auf die Namen der Leiterinnen der o.g. Studie „Viele Welten leben“, so fällt auf, dass eine der beiden Leiterinnen, Frau Prof. Boos-Nünning, schon sein 1999 Mitglied im Bundesjugendkuratorium war.[20] Die zweite Leiterin der Studie, Frau Karakaşoğlu, ist seit 2006 Mitglied des Bundesjugendkuratoriums, in das sie durch die ehemalige Bundesfamilienministerin von der Leyen persönlich berufen wurde.[21] Das Bundesjugendkuratorium kritisiert also zwar zu Recht die ohnehin schon lange bekannten eklatanten Datendefizite bei männlichen Jugendlichen mit Migrationshintergrund, aber verschweigt, dass es eigene Mitglieder waren, die solche einseitigen Studien erstellt haben.

Auch im neuen Koalitionsvertrag der CDU/CSU/FDP-Koalition beschränkt sich die geschlechtersensible Integrationsförderung weiterhin ausschließlich auf weibliche Jugendliche mit Migrationshintergrund:

„Mit dem Programm „Integration durch Sport“ wollen wir besonders Frauen und Mädchen mit Migrationshintergrund ansprechen, um sie als Teilnehmer und auch Übungsleiter zu gewinnen. Wir wollen die Teilnahme zugewanderten Frauen und Mädchen aus allen Kulturkreisen am öffentlichen und gesellschaftlichen Leben fördern. Dafür brauchen wir eine Bildungs- und Ausbildungsoffensive für Migrantinnen.“[22]

Es wird also unverändert ausschließlich eine Bildungsoffensive für Migrantinnen, nicht jedoch für die größten Bildungsverlierer in Deutschland – die Jungen mit Migrationshintergrund – angestrebt.

Doppelmoral in der Rollenbilddiskussion

Jetzt, da der Handlungsbedarf im Bereich der Jungenförderung offensichtlich ist, wird in der Diskussion häufig kurzerhand die Schuld den Jungen selbst zugewiesen und die Behauptung in den Raum gestellt, Jungen seien zu wenig offen für neue Rollenbilder. Dies ist äußert zynisch und verdreht die Realitäten. Denn es waren die politisch Verantwortlichen, die von Beginn an Jungen aus dem größten geschlechterspezifischen Förderprojekt aller Zeiten, das zudem das Berufswahlspektrum und damit die Rollenbilder auf geschlechtsuntypische Berufe erweitern will, gezielt und bewusst ausschlossen – den Zukunftstag. Außerdem sind es ja die Gesellschaft und Politik, die auf die Annehmlichkeiten archaischer Männerrollenbilder – z.B. männliche Zwangsdienstarbeitskräfte im militärischen und sozialen Bereich – nicht verzichten wollen.

So beschränkt sich die heutige staatlich subventionierte „Jungenförderung“ i.d.R. darauf, Jungen zu einer kritischen, ablehnenden Haltung gegenüber ihrer Männlichkeit zu erziehen und in Putz- und Bügelkursen zu tüchtigen Hausmännern zu machen.[23] Und dies, obwohl alle unabhängigen Schulleistungsstudien zeigen, dass Jungen primär Bildungsförderung brauchen. Eine solche Art der „Jungenförderung“ ist jedoch keine echte Jungenförderung, sondern eine profeministisch-ideologisch inspirierte Umerziehung von Jungen, die jungentypische Verhaltensweisen pauschal als defizitär einstuft und somit eine Jungen abwertende Gesellschaft fördert.

Jungen zu mehr Selbständigkeit im Haushalt zu verhelfen, ist ohne Frage sinnvoll. Jungen allerdings exakt die Tätigkeiten als „coole“ Zukunftsperspektiven zu verkaufen, die umgekehrt als Beleg für die Diskriminierung der Frau gelten, ist äußerst fragwürdig.

Diese verkürzte „Rollenbilddiskussion“ wird auch daran erkennbar, dass Jungen zwar dort ihre archaischen Rollenbilder aufgeben sollen, wo sie aus diesen Rollenbildern Vorteile ziehen. So sollen sich z.B. Jungen nicht mehr auf gut dotierte und angesehene Berufe konzentrieren, sondern sich mehr für schlecht bezahlte und schlecht angesehene Berufe entscheiden.

Die Bereiche jedoch, in denen Jungen auf Grund archaischer Rollenbilder Nachteile erleiden, bleiben in der Rollenbilddiskussion ein Tabuthema. So haben z.B. auch die Anhänger der Rollentheorie überhaupt kein Problem mit der einseitigen Männerzwangsdienstkultur (Männerwehrpflicht und Männerzivildienst). Auch das vom Europäischen Gerichtshof für Menschenrechte mehrfach kritisierte und beanstandete, Väter diskriminierende Sorge- und Umgangsrechtswesen in Deutschland ist in der Rollenbilddiskussion ebenso ein Tabuthema wie das Thema Gewalt gegen Jungen und Männer. Dabei wäre gerade die Stärkung der Vaterrolle ein Bereich, der bei einer ehrlichen Rollenbilddiskussion ein Hauptanliegen sein müsste. Und obwohl zwei Drittel aller Gewaltopfer Jungen und Männer sind, werden männliche Gewaltopfer aus der geschlechtersensiblen Gewaltopferbetrachtung ausgeschlossen. Sie werden nicht als Opfer wahrgenommen, sondern lediglich als Versager ihrer Männlichkeit gesehen. Auch daran will die Rollenbilddiskussion nichts ändern.

Weiterhin gibt es derzeit länderabhängig einen Mangel an Fachlehrern. Zudem werden bis zum Jahr 2013 zusätzlich 40.000 Erzieherinnen und Erzieher[24] benötigt. Während in technischen Berufsbereichen speziell Mädchen für diese Berufe angeworben werden, bleibt eine ähnliche Initiative, gezielt Jungen für diese Berufe zu interessieren, aus. Selbst in den stattfindenden Boys-Days werden diese Berufsbereiche häufig ausgeblendet. Auch auf der Homepage des neuen Referates „Gleichstellungspolitik für Jungen und Männer“ des Bundesfrauenministeriums mit Stand vom 10.04.2010 sollen Jungen lediglich für Pflegeberufe und Dienstleistungsberufe gewonnen werden, nicht jedoch für erzieherische oder pädagogische Berufe.

Dies zeigt deutlich, dass es bei der Rollenbilddiskussion nicht um eine echte Emanzipation von Jungen geht, sondern ihnen sollen lediglich die Verliererkomponenten verschiedener Rollenbilder aufgebürdet werden.
 

Sozialisationstheorie als alleingültiges Paradigma

Immer noch werden die wissenschaftlichen Belege, z.B. aus der Evolutionstheorie und Entwicklungspsychologie[25] oder der modernen Hirnforschung[26], relativiert, die zeigen, dass geschlechtstypische Verhaltensweisen und Interessen keineswegs ausschließlich anerzogen sind. So meint Doris Bischof-Köhler:

„Da es fraglich ist, ob sich Männlichkeit in ihren Grundmustern zum Verschwinden bringen lässt – einmal ganz abgesehen davon, ob wir das wirklich für wünschenswert halten -, ist die Gleichberechtigung von Mann und Frau das viel vordringlichere und wahrscheinlich auch realistischere Ziel. Für den Erzieher stellt sich die Herausforderung, dieses Anliegen umzusetzen, dabei jedem Geschlecht in seiner Eigenart gerecht zu werden und dafür Sorge zu tragen, dass keines auf der Strecke bleibt.“[27]

Stattdessen gilt nach wie vor in der politisch geförderten Jungenarbeit die Sozialisationstheorie als allein diskussionswürdiger Erklärungsansatz. Die Sozialisationstheorie ist eine wichtige sozialwissenschaftliche Theorie, welche mit dem Ziel verbunden ist, den „Prozess der Entstehung und Entwicklung der Persönlichkeit in wechselseitiger Abhängigkeit von der gesellschaftlich vermittelten sozialen und dinglich materiellen Umwelt einerseits und der biophysischen Struktur des Organismus andererseits“[28] zu beschreiben und zu erklären. Dieser Theorie liegen allerdings gewisse Einseitigkeiten und Vereinfachungen dort zugrunde, wo sie mit dem Anspruch verwendet wird, die bestimmenden Faktoren für die Herausbildung der Persönlichkeit des Menschen und seines Verhaltens beschränkten sich auf Gesellschaft und Kultur, denen gegenüber biologischen Einflussfaktoren keine (wesentliche) Bedeutung zukomme und die unterschiedliche Psychologie beider Geschlechter außer Acht lässt.

Besonders fatal ist es, wenn die Sozialisationstheorie instrumentalisiert wird, um ein ideologisch vorgefasstes Schubladendenken mit Geschlechterstereotypen von weiblichem Opfergeschlecht einerseits und männlichem Tätergeschlecht andererseits zu rechtfertigen und zu kolportieren.

Anstatt die Sozialisationstheorie als einen Erklärungsansatz von vielen zu berücksichtigen, errang sie in der erziehungs- und sozialwissenschaftlichen Diskussion aber auch in der Pädagogikwissenschaft eine Art Monopolstellung. Hierzu Allan Guggenbühl:

„Die Pädagogischen Hochschulen und die Erziehungswissenschaft sind herausgefordert, eine Schule zu gestalten, in der die Pädagogik und Didaktik beiden Geschlechtern entspricht. In einer eigenartigen Verblendung der psychologischen Realitäten wird immer noch an einseitigen Sozialisations- oder Rollentheorien festgehalten.“[29]

Über die vergangenen Jahrzehnte hat sich eine Jungenarbeit etabliert, die vorrangig ein negatives, defizitäres Jungenbild kolportiert. Ein solch negatives Jungenbild ist natürlich eine äußerst schlechte Basis für eine Jungenförderung. Der Nürnberger Erziehungswissenschaftler Wolfgang Tischner formuliert die Kritik an der Jungenarbeit mit einem negativ besetzten Jungenbild deutlich:

„Unterdessen sollen Jungen mittels profeministischer, antisexistischer und patriarchatskritischer Jungenarbeit lernen, dass sie so, wie sie sind, nicht sein sollten und einem falschen Männerbild hinterherjagten…Jungen sollten sich vom Männlichkeitsdruck befreien […] und letztendlich von einer positiven männlichen Identität verabschieden…Das erste Ziel einer nicht-identitären Jungenarbeit wäre somit nicht der ‘andere Junge‘, sondern gar kein Junge. … Die Adressaten wendeten sich aus guten Gründen ab, wenn Jungenarbeit moralisierend, mit negativen Vorannahmen oder mit Umerziehungsabsichten auf sie zukommt. […] Der Göttinger Jungenpädagoge Götz Haindorff betont deshalb, dass Jungen keine defizitären Wesen seien, die Humanisierungsprogramme benötigen […]. Ohne Liebe und Annahme junger Männer, so sein Fazit, gibt es […] keinen sozialen Prozess mit ihnen. Bestimmte Haltungen und Denkweisen der Jungenarbeit sind daher Teil des Problems, nicht Teil dessen Lösung“.[30]

Wie widersprüchlich eine nicht-identitäre Jungenarbeit ist, kann man an Folgendem erkennen: Trotz der Behauptung, „Geschlecht“ wäre rein konstruiert und nicht von der Biologie abhängig, haben diejenigen, die dies behaupten, kein Problem damit, Kinder und Jugendliche bei Förderprojekten wie dem Zukunftstag oder der MINT-Förderung nach biologischem Geschlecht einzuteilen, wer teilnehmen darf und wer nicht. Wer dies testen will, möge seinen Sohn einmal auf einen Praktikumsplatz für Mädchen am Zukunftstag bewerben lassen mit dem Hinweis, man solle sich vom Geschlechtsteil nicht irritieren lassen, das Kind sei zum Mädchen erzogen worden.

Die unterschiedliche Entwicklung von Mädchen und Jungen ist belegt

Das Bundesjugendkuratorium behauptet, es gäbe keine ausreichenden Hinweise für eine unterschiedliche Entwicklung von Mädchen und Jungen im Vorschulbereich:

„Beleuchtet man Geschlechterdifferenzen im Elementarbereich des Bildungswesens, so gibt es keine geschlechtsspezifischen Unterschiede in der Bildungsbeteiligung und keine uneingeschränkten Belege für Entwicklungsunterscheide zugunsten der Mädchen im Kindergartenalter.“ (Stellungnahme Bundesjugendkuratorium S.11)

Wie das Bundesjugendkuratorium zu dieser Schlussfolgerung gelangt, ist rätselhaft. Die Auswertung der ärztlichen Schuleingangsuntersuchungen, z.B. in Baden-Württemberg oder in Brandenburg, zeigen eindeutig, dass sich Jungen im Bereich Motorik und Sprachfähigkeit tendenziell langsamer entwickeln als Mädchen. Die Untersuchungen in Baden-Württemberg haben gezeigt, dass fast 60% der Jungen zum Zeitpunkt der Einschulung erhebliche Defizite in mindestens einer wichtigen schulischen Grundkompetenz aufweisen.[31] 

Fast doppelt so viele Jungen wie Mädchen landen auf den Sonderschulen. Auch dies belegt die 
signifikanten geschlechtertypischen Unterschiede beim Entwicklungsstand und der Bildungsnachteile von Jungen und Mädchen zum Zeitpunkt der Einschulung und in der Bildungsbeteiligung. Es verwundert, dass diese Erkenntnisse den Fachleuten des Bundesjugendkuratoriums bislang verborgen geblieben sind.

Diese Entwicklungsunterschiede sind eben nicht anerzogen, sondern biologisch gegeben. Hier müsste eine gezielte Förderung von Jungen schon im Vorschulbereich einsetzen, wenn man Jungen gleiche Chancen beim Start in die Schule geben wollte. Stattdessen endet die Politik der Chancengleichheit exakt an dem Punkt, an die die Nachteile und Benachteiligungen von Jungen und Männer beginnen.
Die Aussage der ehemaligen Bundesjugend­ministerin von der Leyen aus der Berliner Zeitung vom 29.09.2006 ist diesbezüglich eindeutig:

„Ich finde es nicht schlimm, dass Mädchen in Sachen Bildung an den Jungen vorbeiziehen.“[32]

Es verwundert nicht, dass das Bundesjugendkuratorium in seiner Stellungnahme auf S.27 im Grunde zu der gleichen Ansicht gelangt wie die Ministerin, die diese Stellungnahme in Auftrag gegeben hat:

„Die Erfolge der Schülerinnen im Bildungssystem in den vergangenen Jahrzehnten sind als Ermutigung zum Abbau von geschlechtsspezifischen Ungleichheiten zu betrachten.“

Hier wird nochmals deutlich, dass die vom Bundesjugendkuratorium kritisierte Verkürzung auf die Jungensituation nicht nur nicht existiert, sondern in der realen Bildungs- und Jugendpolitik sogar in die andere Richtung, nämlich ausschließlich in Richtung auf die Mädchensituation besteht. Die zunehmenden Bildungsmisserfolge von Jungen und die zunehmende Arbeitslosigkeit von männlichen Jugendlichen und jungen Männern werden nicht als Problem gesehen, sondern als positive Rückmeldung einer Geschlechterpolitik verstanden, die sich auch heute noch ausschließlich auf die „Frauenfrage“ beschränkt.

Vernachlässigung der Leseförderung von Jungen

Tim Rohrmann hebt die besondere Bedeutung der Jungenleseförderung hervor:

„Unter Fachleuten besteht Übereinstimmung darin, dass Bemühungen um einen Ausgleich der Benachteiligung von Jungen entscheidend an der Lesemotivation und an den Leseaktivitäten ansetzen müssen. Vor diesem Hintergrund wird eine geschlechterreflektierende Lese- und Schreibförderung gefordert, die besonders für Jungen neue Wege einschlagen muss.“[33]

Die geschlechterspezifischen Unterschiede bei den 15-Jährigen sind laut PISA-Studien 2000, 2003 und 2006 jedoch nahezu gleich geblieben. So betrug im Jahr 2000 der Unterschied in der Lesekompetenz aus der PISA-Studie noch 35 Punkte zuungunsten der Jungen. Im Jahr 2003 stieg er schon auf 42 Punkte[34] und im Jahr 2006 blieb er unverändert bei 42 Punkten[35].

Entgegen dieser Erkenntnisse relativiert das Bundesjugendkuratorium in seiner Stellungnahme die geschlechterspezifischen Unterschiede in der Lesekompetenz:

„Zwar ist nachgewiesen, dass Mädchen gegenüber Jungen im Grundschulalter einen Vorsprung in der Lesekompetenz haben, zugleich allerdings lässt sich belegen, dass sich dieser Leistungsvorsprung der Mädchen zwischen 2001 und 2006 nahezu halbiert hat.“

Wie kommen diese Diskrepanzen bei den Lesekompetenzbewertungen zustande?
Zur Lesekompetenz liegen zwei wesentliche internationale Vergleichsstudien vor, die IGLU-Studie (Internationale Grundschulleseuntersuchung) und die PISA-Studie. Ein wesentlicher Unterschied besteht darin, dass die IGLU-Studie mit Viertklässlern durchgeführt wird, also mit Schülern und Schülerinnen im Alter von etwa 10 Jahren, die PISA-Studie jedoch mit 15-Jährigen. Nun sind die geschlechterspezifischen Unterschiede bei der IGLU-Studie (10-Jährige) wesentlich geringer als bei der PISA-Studie (15-Jährige). Dies bedeutet, dass sich die geschlechterspezifischen Unterschiede im Lesen nicht reduzieren, sondern während der Schulzeit noch deutlich zunehmen. Dies ist das Scheitern eines Bildungssystems und eines Bildungswesens, die sich Geschlechtergleichstellung auf ihre Fahnen geschrieben haben.

Die einseitige Betrachtung lediglich der Grundschulergebnisse, bei gleichzeitigem Vorenthalten der Lesekompetenzunterschiede am Ende der Hauptschule, ist nicht nur ein deutlicher Hinweis, dass die Stellungnahme des Bundesjugendkuratoriums nicht bestrebt ist, die Bildungssituation von Jungen umfassend und objektiv darzustellen, sondern sie zu relativieren. Die Lesekompetenz ist aber nicht nur im Grundschulalter wichtig, sondern gerade zum Ende der Schule und damit für die erfolgreiche Integration ins von den Eltern unabhängige gesellschaftliche und berufliche Leben.

Das Thema Jungenleseförderung wird von der Fachwelt seit Jahren heftig diskutiert. Die Bildungspolitik hat sich dieser Herausforderung bislang allerdings nicht ernsthaft gestellt. Dabei ist der geeignete Ansatz zur Jungenleseförderung schon lange bekannt, denn bei gleicher Motivation (Lesefreude) zeigen Jungen gleiche Leistungen wie Mädchen.[36] Das heißt, eine Verbesserung der Lesekompetenz ist über eine Verbesserung der Leselust bei Jungen erreichbar. Aber:

„Die Auswahl von stark mädchenorientierter Literatur in Grundschulen spricht die wenigsten Jungen an und gibt ihnen damit kaum Möglichkeiten zur Stärkung ihrer Lesekompetenz.“[37]

Eine der führenden Kapazitäten der geschlechterspezifischen Leseförderpädagogik, Christine Garbe, meint:

„Die sozialen Kontexte und Institutionen sowie die medialen Angebote im Printmedienbereich, die Prozesse der Lesesozialisation in der Kindheit und Jugend modellieren, bedienen heutzutage die Interessen von Mädchen besser als die der Jungen. Die vielfach diagnostizierte Leseschwäche und Leseunlust der Jungen sind eine Folge dieses Sachverhalts. Hier gilt es in Zukunft energisch umzusteuern.“[38]

Verkürzungen in der Diskussion zur Mathematikförderung

Bezeichnenderweise missachtet das Bundesjugendkuratorium selbst seinen eigenen Appell zur differenzierten Sichtweise exakt dort, wo es auf Nachteile von Mädchen hinweist.

„Für höhere Altersgruppen lässt sich zudem nachweisen, dass Schüler beispielsweise ausgeprägtere mathematische Kompetenzen haben als Schülerinnen. Hier erreichen sie im Sekundarbereich im Vergleich der OECD-Länder (in 23 von 30) signifikant bessere Leistungen als Mädchen, wobei Deutschland im OECD-Durchschnitt liegt.“[39]

Die Behauptung, Jungen zeigten in Mathematik bessere Leistungen, ist jedoch zu undifferenziert. Tatsache ist, dass die durchaus besseren Durchschnittswerte der Jungen im Bereich der mathematischen Kompetenz durch die außerordentlichen Spitzenleistungen einiger weniger Schüler zustande kommen, während auch in der Mathematik, in den Naturwissenschaften und sogar beim Umgang mit dem Computer der Anteil von Jungen in der untersten Kompetenzstufe zumindest gleich, meist jedoch sogar höher ist als der der Mädchen.[40]

Durch die einseitige Fixierung in der Mathematik, den Naturwissenschaften oder im Computerumgang auf Mädchenförderung werden die männlichen Risikoschüler zusätzlich benachteiligt. Was geschieht mit diesen Jungen, die entgegen dem Klischee eben nicht als Mathematikgenies oder Computerfachmänner geboren werden und wegen ihres Geschlechts aus den Fördermaßnahmen ausgeschlossen werden? Sie fallen durch das Gender-Netz und bleiben in der Bildung zurück. Hier wird derzeit eine neue Generation Bildungsverlierer geschaffen.
 

Bildungsmisserfolge von Jungen als „positive Diskriminierung“

Es existieren deutliche Hinweise, dass die zunehmenden Bildungsmisserfolge der Jungen von der Bildungs- und Jugendpolitik zumindest teilweise als „positive Diskriminierung“ im Sinne der Frauenförderung gesehen werden.

„Köhler sowie Tischner gehen davon aus, dass diese Benachteiligung von manchen Politikerinnen im Sinne einer positiven Diskriminierung von Mädchen bewusst in Kauf genommen wird. Dabei werden sie auch aus der Genderforschung heraus unterstützt, wie aktuellste Veröffentlichungen zum Thema Geschlecht und Bildung zeigen. Beispielsweise geht es in dem Handbuchartikel von Kaiser (2008) Geschlechtergerechte Schule – eine Chance für Mädchen (und Jungen) – die Klammer wurde tatsächlich so von der Autorin gesetzt – ausschließlich um die Kaiser zufolge immer noch benachteiligten Mädchen.“[41]

Im Juli 2003 bestreitet Waltraut Cornelißen, Leiterin der Abteilung Geschlechterforschung und Frauenpolitik am Deutschen Jugendinstitut in München, also dem Institut, das das Bundesjugendkuratorium in seiner Arbeit unterstützt, in der Frankfurter Rundschau keineswegs, dass das Schulwesen heute durchaus die Entwicklung von Jungen hemmen könne.[42] Doch sieht sie diesen Bildungsrückstand der Jungen aus Gründen der Unterstützung von Mädchen als „bitter notwendig“.
Auch das Bundesjugendkuratorium lässt keinen Zweifel, dass es sich weniger um die Bildungsmisserfolge von Jungen sorgt, sondern vielmehr um die Nutzung dieser Bildungsrückstände der Jungen durch die Mädchen:

„Weiterhin wäre in Studien zu untersuchen, ob der in Teilen belegte Vorsprung der Mädchen und jungen Frauen innerhalb des Bildungssystems in späteren Lebensabschnitten auch eingelöst werden kann, ob also bessere Leistungen und höhere Abschlüsse zukünftig zu entsprechenden beruflichen Karrieren führen.“[43]

Als Rechtfertigung dafür wird eine generelle Benachteiligung von Frauen im Berufsleben postuliert. Aber auch diese einseitige Sichtweise entbehrt die vom Bundesjugendkuratorium selbst geforderte Differenziertheit. Die männliche Jugendarbeitslosenquote ist nämlich je nach Bundesland heute um 20 bis 40 % höher ist als die weibliche Jugendarbeitslosenquote.[44] Eine Tatsache, die sich mittlerweile auch auf den Gesamtarbeitsmarkt durchgeschlagen hat. Hier ist die Männerarbeitslosenquote heute höher als die Frauenarbeitslosenquote.[45] Auch diese höheren Arbeitslosenzahlen blieben den Fachleuten des Bundesjugendkuratoriums bislang offenbar verborgen.

Jungen darf nicht zum Vorwurf gemacht werden, dass sich Mädchen „bei ihrer Berufswahl auf ein kleines Spektrum der anerkannten Ausbildungsberufe“[46] beschränken. Schule hat die Aufgabe, Jungen und Mädchen gleichermaßen optimal zu fördern und keine „ausgleichenden“ Bildungsunterschiede im Hinblick auf eventuell späteres Berufswahlverhalten zu schaffen. Wenn es Hinweise gibt, dass ein Geschlecht Nachteile in der Bildung erfährt, sind die Ursachen zu eruieren und zu beseitigen, unabhängig vom Geschlecht.

Die Bildung als Jungenverliererin

Von 1995 bis 2005 ist die Absolutzahl männlicher Studienabschlüsse im Bereich Ingenieurwesen um 30% gesunken.[47] Michael Matzner und Wolfgang Tischner konkretisieren:

„So schlossen im Jahr 2004 lediglich 25 375 Männer ein Studium der Ingenieurwissenschaften erfolgreich ab, im Jahr 1995 betrug diese Zahl noch 40 600. Im gleichen Zeitraum stieg die entsprechende Zahl nur recht gering an, von 6 600 auf 7 461.“[48]

Klaudia Schultheis hebt den bedürfnisorientierten Ansatz deutlich hervor:

„In Untersuchungen zu schulischen Interessens- und Bedürfnisstrukturen weiblicher und männlicher Schüler …wurde deutlich, dass Jungen sowohl hinsichtlich unterrichtsorganisationaler wie auch unterrichtsstruktureller Maßgaben für eine schulische Zufriedenheit anders gelagerter Notwendigkeiten bedürfen als Mädchen. So benötigen sie beispielsweise mehr Pausen und Bewegung, eine erhöhte Strukturierung des Lernstoffes, mehr Instruktionen sowie klarere Rahmenbedingungen, Strukturen und Ziele. Angesichts der vielfältigen Debatten um schulische Benachteiligungsstrukturen männlicher Schüler kommt dieser Forschungsrichtung erhöhte Relevanz zu.“[49]

Ein Beispiel: Während zu Beginn der Schulzeit fast 80% der Jungen sagen, sie würden gerne lesen, behaupten dies zum Ende der Schulzeit nur noch weniger als 20%[50].

Diese Daten zeigen, dass die Jungen nicht nur Bildungsverlierer sind, sondern die Bildung ist eine Jungenverliererin. Sie schafft es nicht, Jungen adäquat anzusprechen und deren Bildungspotenzial auszuschöpfen. In diesem Zusammenhang ist die dreiste Behauptung, Jungen seien selber schuld an ihrer Bildungsmisere, weil sie weniger Leistungsbereitschaft zeigen würden, völlig unqualifiziert. Nicht nur, dass die pauschale Behauptung, Jungen seien fauler als Mädchen, jungendiskriminierend ist. Jungen sind Kinder und was aus Kindern wird, dafür sind wir Erwachsenen verantwortlich, nicht die Kinder und wenn unser Bildungswesen nicht fähig ist, Jungen zu motivieren, liegt das nicht an den Jungen. Die Schule ist für die Kinder da, nicht umgekehrt.
 

Einige kritische Themen bleiben unerwähnt

Bei der Stellungnahme des Bundesjugendkuratoriums fällt auf, dass wichtige Themen, die für die Bildungsförderung von Jungen direkt oder indirekt wichtig sind, nicht genannt werden.

• Schlechtere Noten für Jungen bei gleichen schulischen Kompetenzen

Was das Bundesjugendkuratorium komplett verschweigt, ist der Befund, dass Jungen bei gleichen schulischen Kompetenzen schlechtere Noten erhalten und bei gleichen Noten seltener an höher führende Schulen empfohlen werden als Mädchen.[51] Hierzu nochmals Michael Matzner und Wolfgang Tischner:

„Eine weitere Form der Diskriminierung, Disziplinierung und Bestrafung von Jungen besteht in der schlechteren Benotung – und zwar unabhängig von den tatsächlich erbrachten Schulleistungen – und damit unter Umständen der Vorenthaltung von Bildungschancen: In allen Fächern erhalten Jungen auch bei gleichen Kompetenzen schlechtere Noten. Jungen werden auch bei gleichen Noten […] seltener von den Lehrkräften für gymnasialgeeignet angesehen als Mädchen… Man stelle sich nur die Empörung vor, wenn davon Mädchen betroffen wären.“[52]

Die Qualität der Geschlechterpolitik wird sich daran messen lassen müssen, inwieweit sie auch die Benachteiligung von Jungen in den Blick nimmt. Dies ist jedoch nicht erkennbar:

„In anderen Veröffentlichungen […] wird die Tatsache der systematischen Benachteiligung von Jungen von Jungen im Bildungswesen relativiert und Jungenförderung auf eine männerkritische Perspektive hin orientiert, bei der es darum gehe, eine Remaskulinisierung der Jungen zu verhindern. Jungen sollten keine spezifisch männliche Identität entwickeln, da dies Frauen und Mädchen schade.“[53]

In dieser Hinsicht muss man der Geschlechterpolitik in der „Jungenfrage“ ein Scheitern konstatieren.

• ADHS

Aber auch andere kritische Themenbereiche, die diskussionswürdig sind, bleiben in der Stellungnahme des Bundesjugendkuratoriums unerwähnt, z.B. ADHS – ein Thema, das auch die Schule betrifft. Immerhin sind mindestens etwa 5% der Jugendlichen davon betroffen,[54] mehrheitlich Jungen.[55] 

Jungen werden viermal häufiger dagegen medikamentös behandelt als Mädchen.[56] Diese Entwicklung ging an den Fachleuten des Bundesjugendkuratoriums bislang offenbar vorbei. Ist es wirklich nur eine Modekrankheit, wie manche Leute behaupten, und missbrauchen wir Medikamente, um unbequeme Kinder, hauptsächlich Jungen, gefügiger zu machen, quasi als pharmazeutischen Rohrstock unserer „humanen“ Zeit? Oder ist es wirklich eine Krankheit und tut man Jungen unrecht, wenn man ihre oftmals auffälligere Unruhe wegsozialisieren will? Oder liegt die Wahrheit irgendwo dazwischen? Das sind Fragen, deren Antworten auch für die Bildungsförderung wichtig sind. Leider wird das Thema derzeit vorrangig von der pharmazeutischen Industrie bearbeitet. Hier wäre es wichtig, dass die Politik für unabhängige Studien sorgt, die betroffenen Eltern Sicherheit bei ihren Entscheidungen gibt und den nebulösen Charakter von ADHS beseitigt.
 

Alle Jungen sind von den Nachteilen und Benachteiligungen betroffen

Das Bundesjugendkuratorium kritisiert auf S. 25 seiner Stellungnahme, dass insbesondere der mediale Diskurs, aber auch in Teilen die wissenschaftliche Debatte über Bildungsungleichheiten zu verkürzt auf die Kategorie Geschlecht dargestellt würde. Dadurch würden andere Faktoren nicht hinreichend berücksichtigt. Diese Auffassung klingt in einer Gesellschaft, die Gleichberechtigung ausschließlich an Frauenquoten misst und die Förderung im MINT-Bereich von weiblichen Geschlechtsmerkmalen abhängig macht, äußerst fadenscheinig.

Ein großer Irrtum beim Thema Jungenförderung besteht zudem darin, dass der Förderbedarf oft nur für Jungen mit niedriger sozialer Herkunft oder für Jungen mit Migrationshintergrund konstatiert wird. So meint das Bundesjugendkuratorium:

„Zudem ist es nicht zutreffend, »die« Jungen pauschal als Bildungsverlierer zu betrachten, da die Ergebnisse für die Gruppe der Jungen ein sehr heterogenes Bild abgeben, insbesondere wenn weitere Unterscheidungen nach Migrationsgeschichte und sozialer Herkunft berücksichtigt werden.“[57]

Diese Annahme trifft aber nur dann zu, wenn man die Absolutzahlen betrachtet. Betrachtet man jedoch die geschlechterspezifischen Benachteiligungen von Jungen gegenüber Mädchen, sind Jungen ohne Migrationshintergrund und mit Eltern mit mittleren Schulabschlüssen am stärksten betroffen. Heike Diefenbach führt dazu aus:

„Der „Armensohn mit Migrationshintergrund“ […] ist in der gesamten Schülerschaft an allgemeinbildenden Schulen in Deutschland der Typus von Schüler, der die meisten Risikofaktoren für eine erfolgreiche Bildungslaufbahn auf sich vereinigt, wenn man sie unabhängig voneinander betrachtet. Will man aber die Gruppe der männlichen Schüler an deutschen allgemeinbildenden Schulen benennen, die die größten Nachteile gegenüber weiblichen Schülern haben, dann handelt es sich um die Söhne von Eltern, mit mittlerer Bildung ohne Migrationshintergrund. Die Diskussion um das Thema „Geschlecht und Bildung“ enthalten viele Missverständnisse, die dadurch zustande kommen, dass diese beiden Schülertypen nicht auseinandergehalten werden oder nicht hinreichend deutlich gemacht wird, wann von dem einen und wann von dem anderen Schülertyp die Rede ist.“ [58]

Auch die Notwendigkeit einer Förderung von Jungen in den Bereichen Sprachfähigkeit oder Motorik schon im Vorschulbereich auf Grund der tendenziell langsameren Entwicklung von Jungen in diesen Kompetenzen tangiert die Jungen aus allen Bereichen. Ebenso betrifft die Lesemotivation als Leseförderung durchweg alle Jungen. Auch die Benachteiligung durch die schlechtere Notenvergabe an Jungen trotz gleicher schulischer Kompetenzen tangiert alle Jungen.

Die Aussage des Bundesjugendkuratoriums, dass Bildungserfolg nicht nur vom Geschlecht abhängt, ist durchaus richtig, aber er hängt auch vom Geschlecht ab. Insgesamt kann man resümieren, dass Bildungserfolg in Deutschland vom Migrationshintergrund, von der sozialen Stellung der Eltern UND vom Geschlecht abhängt.

Gender Mainstreaming

Das Bundesjugendkuratorium schlägt als Lösung u.a. vor, die Ansprüche des Gender Mainstreaming umzusetzen und zu einem Managing Diversity weiterzuentwickeln. Mit dem Konzept des Gender Mainstreaming läge ein geschlechterthematischer Handlungsansatz vor, der es ermögliche, mit der im Diskurs um die Bildungsbenachteiligung von Jungen diskutierten Problematik kompetent und zielführend umzugehen. Die Anhänger dieser geschlechterpolitischen Strategie betonen, dieser Ansatz würde auch die legitimen Anliegen und Belange von Jungen und Männern berücksichtigen. Ein hehrer Anspruch, an dem Gender Mainstreaming bislang allerdings in allen Bereichen durchweg gescheitert ist – in der Gesundheitspolitik, in der Familienpolitik und auch in der Bildungs- bzw. Jugendpolitik.

Werfen wir einen Blick auf die konkreten Maßnahmen, die hinter dem Begriff „Gender Mainstreaming“ stecken. Das Deutsche Jugendinstitut (DJI), das ja, wie schon erwähnt, das Bundesjugendkuratorium unterstützt – der Leiter des DJI hat den Status eines „ständigen Gastes“ beim Bundesjugendkuratorium –, hat sich ebenfalls dem Gender Mainstreaming verschrieben. Die dortige Datenbank PRAXIMO wurde um ein Modul “Gender Mainstreaming” erweitert. Aufgabe des Projektes ist es, durch systematische Recherche, Auswertung und gezielte Verbreitung von innovativen Praxismodellen Anregungen für die Anwendung der Strategie Gender Mainstreaming im Arbeitsfeld Jugendsozialarbeit zu geben.[59]

Dann werden vier Konzepte aufgelistet, von denen die ersten beiden Punkte durchaus Mädchen und Jungen betreffen (Konzepte, mit denen Mädchen und Jungen befähigt werden, Erwerbs- und Familienarbeit in ihre Lebensplanung erfolgreich zu integrieren und Konzepte, die die Erweiterung der Handlungsmöglichkeiten jenseits geschlechtstypischer Einengungen ermöglichen).

Gerade aber im Bildungsbereich reduziert sich dieser Gender Mainstreaming-Ansatz wieder auf die reine Frauen- und Mädchenförderung der letzten 30 Jahre. So sollen im Sinne dieses vom DJI interpretierten Gender Mainstreaming lediglich Strategien entwickelt werden, „die die Benachteiligung von Mädchen und Frauen in Ausbildung und Erwerbsarbeit überwinden“.

Das Bundesjugendkuratorium gibt an, dass sich der Unterschied in der Ausbildungsbeteiligung zwischen Mädchen und Jungen zuungunsten der Mädchen von 2004 bis 2006 vergrößerte. Ebenfalls zeige das Panel auf, dass Jungen mit Hauptschulabschluss trotz schlechterer schulischer Voraussetzungen bessere Chancen als Mädchen haben, ohne Zwischenschritte eine Berufsausbildung zu beginnen.[60] Dies ist eine Verdrehung der Realität. Die Tatsache, dass Jungen schlechtere Bildungsabschlüsse haben als Mädchen und damit seltener weiterbildende Wege wie z.B. ein Studium einschlagen können und damit folgerichtig häufiger Ausbildungsberufe belegen, wird den Jungen hier kurzerhand als Vorteil interpretiert. Zudem werden auch hier die männerspezifischen Probleme beim Übergang von Ausbildung zu Beruf völlig außer Acht gelassen, die durch den gerade in der deutschen Politik ausgeprägten Hang zur Männerzwangsdienstkultur geschaffen wird.

Auch die ausschließlich auf Mädchenförderung ausgerichtete, aktuelle geschlechterspezifische Förderpolitik in den Pädagogischen Hochschulen in Baden-Württemberg, wie oben beschrieben, zeigt das Versagen von Gender Mainstreaming in der Praxis, indem es sich bei der konkreten Umsetzung doch wieder ausschließlich in Mädchenförderprojekten erschöpft.

Obwohl sich alle Parteien zum Prinzip des „Gender Mainstreaming“ bekennen und „Gender Mainstreaming“ im Vorfeld aller politischer Entscheidungen dafür sorgen soll, dass die Anliegen und Belange beider Geschlechter berücksichtigt werden sollen, steht z.B., wie vorher schon erwähnt, im Koalitionsvertrag der schwarz-gelben Bundesregierung beim Stichwort „Integrationspolitik“ lediglich die Forderung nach einer Bildungsoffensive für Migrantinnen, obwohl eindeutig belegt ist, dass die männlichen Jugendlichen mit Migrationshintergrund die Klientel mit den größten Bildungsproblemen ist.

Die Grundlage von „Gender Mainstreaming“ ist die sogenannte „Genderanalyse“, bei der die Ausgangslage bei-der Geschlechter analysiert und die Auswirkung der Maßnahme auf beide Geschlechter abgeschätzt werden muss. Gerade auch diejenigen Einrichtungen, die „Gender Mainstreaming“ vehement propagieren, ignorieren diese Basis von „Gender Mainstreaming“. So unterbreiteten die Sozialministerinnen Stolz (CDU), Baden-Württemberg, und Haderthauer (CSU), Bayern, auf der 86. Arbeits- und Sozialministerkonferenz (ASMK) am 21. und 22. Oktober 2009 in München unter TOP 4.15 folgenden Beschlussvorschlag:
 
 „Die Amtschefinnen und Amtschefs für Arbeit und Soziales der Länder empfehlen der ASMK folgenden Beschluss:

Die Ministerinnen und Minister, Senatorinnen und Senatoren für Arbeit und Soziales der Länder bitten das Bun-desministerium für Arbeit und Soziales zur Erlangung einer verlässlichen Datengrundlage einen Forschungsauftrag zu erteilen, der die Situation von Frauen und Mädchen mit Migrationshintergrund unter den Merkmalen Geschlecht, Ethnizität und Diskriminierungserfahrungen analysiert. Schwerpunkte der Forschung sollen der Zugang zu Bildung, zum Arbeitsmarkt sowie gesellschaftliche und politische Partizipation sein.

Die Programme und Maßnahmen zur Integration können sich ohne eine verlässliche Datengrundlage und Aus-ganganalyse nicht auf die besonderen Lebenslagen und Lebenswirklichkeiten von Frauen und Mädchen mit Migra-tionshintergrund einstellen.“

Zur Begründung führen die Ministerinnen Stolz und Haderthauer an:

„Derzeit liegen so gut wie keine Daten zu den Lebenslagen von Frauen und Mädchen mit Migrationshintergrund vor. Es ist nur wenig über ihre Chancen auf Bildung, Zugang zum Arbeitsmarkt und sowie Teilhabe am gesell-schaftlichen und politischen Leben bekannt.

Die Programme und Maßnahmen zur Integration können sich ohne eine verlässliche Datengrundlage und Aus-ganganalyse nicht auf die besonderen Lebenslagen und Lebenswirklichkeiten von Frauen und Mädchen mit Migra-tionshintergrund einstellen. Auch zur Durchführung positiver Maßnahmen wird eine verlässliche Datenbasis benö-tigt. Die Analyse spezifischer Problemlagen sowie spezifischer Lösungsansätze dienen der Integration dieser Frauen und Mädchen sowie der Herstellung von Chancengleichheit.“

Obwohl davon auszugehen ist, dass beide Sozialministerinnen über die Datendefizite von männlichen Jugendlichen mit Migrationshintergrund Kenntnis besitzen und obwohl ebenso davon auszugehen ist, dass beide Sozialministerinnen wissen, dass fast jeder vierte männliche Jugendliche mit Migrationshintergrund die Schule in Deutschland ohne einen Abschluss verlässt, schenken sie bei der Datenerhebung der Situation von männlichen Jugendlichen mit Migrationshintergrund keinerlei Beachtung.

Gleichwohl wollen sie für Frauen und Mädchen Chancengleichheit herstellen. Chancengleichheit mit wem? Chancengleichheit auf welchen Gebieten? Da die Lebenslagen der männlichen Migranten ebenso im Dunkel liegen wie die der Migrantinnen, können die avisierten „positiven Maßnahmen“ zur Migrantinnenförderung de facto nur darauf hinauslaufen, auf willkürlich festgelegten Gebieten mit willkürlich festgelegten Maßnahmen zu willkürlich festgelegten Zielen mit völlig unbekannter Wirkung im Hinblick auf die tatsächliche Gleichstellungssi-tuation und ausschließlich frauenbezogen aktiv zu werden. Für diese a priori festgelegte Gleichstellungspolitik bräuchte es an sich überhaupt keine empirischen Daten. Dafür genügte ein Glaubensbekenntnis.

Allein schon an diesen beiden für die Bildung relevanten Beispielen der realen Integrationspolitik ist erkennbar, dass „Gender Mainstreaming“ in Bezug auf die versprochene gleichberechtigte Berücksichtigung jungen- und männerrelevanter Anliegen und Belange nicht das Papier wert ist, auf dem es geschrieben steht und zwangsläu-fig ins Leere gehen muss. So sieht „Gender Mainstreaming“ in der Praxis aus. Solange Jungen die Verlierer sind, ist die „Gender-Mainstreaming“-Welt in Ordnung.

In Ergänzung dazu möchten wir darauf hinweisen, dass in Nordrhein-Westfalen das Hauptreferat „Gender Main-streaming“ im Bereich der Jugendarbeit ausgerechnet im Verein „Frauen unterstützen Mädchenarbeit FUMA e.V.“ implementiert wurde. Dies zeigt u.E. deutlich, wer „Gender Mainstreaming“ macht und für wen „Gender Mainstreaming“ gemacht wird.
 

„Girls’ Day“ und „Neue Wege für Jungs”

In der Stellungnahme des Bundesjugendkuratoriums wird im Punkt „Geschlechtsspezifische Selektion im Berufswahlverhalten überwinden!“ u.a. gefordert, Projekte wie den »Girls’ Day« und »Neue Wege für Jungs« zu verstärken und auszubauen. Dies begrüßen wir. Was das Bundesjugendkuratorium jedoch verschweigt: Es war gerade die Bundesjugendpolitik, die Jungen von Beginn an die Teilnahme am „Zukunftstag“ (Girls‘ Day), eben einer solchen Maßnahmen zur Erweiterung des Berufswahlspektrums auf geschlechtsuntypische Berufsbereiche, verwehrt hat. Diese Ausgrenzung hält in 13 von 16 Bundesländern bis heute an. Nur Niedersachsen, Brandenburg und offiziell auch Sachsen-Anhalt führen einen Zukunftstag für Mädchen UND Jungen durch.

Statt den Ausschluss von Jungen aus dem Zukunftstag zu beenden, wurde ein anderes Projekt – „Neue Wege für Jungs“ – eingeführt, im Rahmen dessen auch sogenannte Boys‘ Days durchgeführt werden sollen. Dieses Nebeneinander von „Girls‘ Day“ und „Boys‘ Days“ suggeriert eine Gleichrangigkeit, ja sogar eine Gleichwertigkeit dieser beiden Maßnahmen, die jedoch nicht gegeben ist. Während der Girls’ Day ein gewaltiges, mit vielen Fördermitteln versehenes Megaevent darstellt, stellen die „Boys’ Day“-Bemühungen im Rahmen des Projektes „Neue Wege für Jungs“ daneben allenfalls ein kleines Abziehbild dieses Megaevents dar, das die Ausgrenzung der Jungen aus dem Zukunftstag, wie der Girls‘ Day auch noch heißt, eher festzementiert, anstatt sie zu beenden. Vergleicht man die Praktikumsplätze in der bundesweiten Girls‘ Day-Datenbank mit den Praktikumsplätzen beim Boys’ Day aus der „Respekt-Jungs“-Datenbank z.B. bei der Stadt Karlsruhe, beträgt das Verhältnis von Mädchenplätzen zu Jungenplätzen Stand Ende 2009 etwa 1000 zu 1[61] zuungunsten der Jungen. Von einer Gleichwertigkeit kann also überhaupt nicht die Rede sein.

Weiterhin sind auch die Konzepte völlig verschieden. So ist der Girls’ Day eine Veranstaltung, die den Mädchen die gut bezahlten frauenunterrepräsentierte Berufsbereiche vorstellen will. Beim Boys’ Day dagegen werden Jungen i.d.R. nicht alle männerunterrepräsentierten Berufsbereiche vorgestellt, sondern lediglich die Bereiche, die eher niedrig entlohnt werden und/oder wenig Aufstiegschancen bieten – kurz gesagt, die Berufsbereiche, die man Mädchen nicht mehr zumuten möchte. Attraktive frauendominierte Ausbildungs- und Berufsbereiche, wie im Bereich Dienstleistungswesen, Finanzwesen oder Medizin / Veterinärmedizin werden in der Regel nicht berücksichtigt. Selbst pädagogische Berufe sind ein Tabuthema. Viele Kritiker sehen deshalb die Boys’ Days als „Billigjobbörse“ für Jungen. Eine Kritik, die in der pauschalen Form sicherlich ungerechtfertigt ist, aber durch die einseitige Ausrichtung natürlich kolportiert wird.

MANNdat begrüßt ausdrücklich die Erweiterung des Berufswahlspektrums für Jungen auf geschlechteruntypische Berufsbereiche. MANNdat ist deshalb seit Beginn der Ausgrenzung von Jungen aus dem Zukunftstag einer der größten Kritiker dieser Ausgrenzung. Aber diese Berufswahlerweiterung sollte nicht ideologisch inspiriert sein, sondern alle Branchen und damit auch die gut bezahlten Frauenberufe beinhalten. Wir lehnen jedoch einen Boys’ Day ab, der lediglich eine Billigjobbörse für Jungs darstellt.

Hinzu kommt, dass wichtige Hemmnisse für eine Erhöhung des Männeranteils in erzieherische, pädagogische oder soziale Berufe bislang ein Tabuthema in der Diskussion darstellen. So hat z.B. der Mobbingreport der BAUA 2008 gezeigt, dass vor allem männliche Erzieher unter Mobbingproblemen leiden.[62] Zudem gibt es mittlerweile Urteile von Verwaltungsgerichten, die die Ablehnung von männlichen Erziehern auf eine Erzieherstelle auf Grund des männlichen Geschlechts als zulässig sehen.[63] Dies weist darauf hin, dass der Mangel an männlichen Erziehern weniger an festgefahrenen Rollenbildern der Jungen begründet liegt, sondern an den Vorurteilen gegenüber männlichen Erziehern und Lehrern. Die Erziehungskompetenz von Männern wird in unserer Gesellschaft ebenso wenig anerkannt wie ihre pädagogische Unentbehrlichkeit für Kinder und Jugendliche, insbesondere Jungen. Hier gilt es, Vorurteile und Diskriminierungen abzubauen.

Männlichkeitsabwertung im Erziehungswesen

In der Bildungsdiskussion werden die Kindergärten, oder Kindertagesstätten, wie es heute heißt, oftmals übersehen. Dabei fängt Bildung im Kindergarten an. Aber auch dort ist die Situation nicht unbedingt jungenfreundlicher.

Auf einer Kindergärtnerinnensynode in Winterthur 1991 empfahl Prof. Dr. Luise Pusch einer Teilnehmerin, die Bedenken geäußert hatte, Jungen im Kindergarten zu brüskieren oder bloßzustellen den Jungen sogar „Wunden“ zuzufügen. „Diese Verletzungen würden sowieso zu schnell wieder verheilen“[64]

Hat sich seit 1991 an dieser jungenabwertenden Einstellung in den Erziehungswissenschaften etwas geändert? Leider nicht sehr viel. Im Februar 2010 erschien im Verlag Cornelsen Scriptor das Buch „Kinder erziehen, bilden und betreuen – Lehrbuch für Ausbildung und Studium“. Das Buch wird auf der Bildungsserverplattform „Bildungsklick“ angepriesen und soll der Erzieherinnenausbildung dienen. Schon das Cover verrät, dass der Verlag Erziehung als Frauensache sieht. So sind nur Erzieherinnen und Kinder, aber keine Erzieher abgebildet. Das Buch hebt zudem ab auf eine ins Groteske überspitzte Sozialisationstheorie mit jungen- und männerfeindlicher Ausrichtung bei der pauschal in eine „gute Frauenwelt“ und eine „schlechte Männerwelt“ polarisiert wird. Auf den Seiten 143 und 144 finden sich z.B. folgende Textpassagen:

„Noch immer gelten weitgehend die alten patriarchalischen, hierarchischen Konstrukte, wonach das Mädchen passiv, dienend, pflegend, anpassend, attraktiv usw. zu sein hat, der Junge dagegen aktiv, aggressiv, stark, durchsetzungsfähig usw….. Die Situation der Mädchen ist trotz gesetzlicher Gleichberechtigung schlecht.“
„ …Tatsächlich leiden Mädchen auch unter einer generalisierten Gewalt, die sich im Patriarchat ausdrückt.“ 

Die Gewalt im einzelnen:

„ …ökonomische Gewalt, die Mädchen von den Vätern oder späteren Arbeitgebern abhängig macht (weniger bezahlt, zuerst entlassen)
„…soziale Gewalt..ausgeübt durch …Kleidervorschriften..und ältere Brüder…“
„Körperliche Gewalt…in der Hauptschule…“
„Sexuelle Gewalt zeigt sich im grausamen Besitzdenken des Mannes gegenüber dem Körper der Mädchen…die durch ihn Demütigung, Schmerzen und Ohnmacht erleiden.“
„Seit der Entstehung des Patriarchats zwischen 1200 und 750 v.Chr. schufen Männer die Vorstellung der superioren (überlegenen) Männlichkeit und der inferioren (unterlegenen) Fraulichkeit. Solch ein jahrtausendealtes Mädchen- und Frauenverständnis wirkt bis heute nach.“ … „Noch immer entwickeln Jungen oft nach altem Muster Dominanzverhalten und mangelnde Sozialkompetenz. Darum halten sie sich wenig an Regeln und beanspruchen vor allem in der unteren Schicht Dominanz, was sich in disziplinlosem Verhalten ausdrückt.“

Verantwortlicher Autor für dieses Kapitel ist Prof. Dr. Winfried Noack. Schon allein an diesen Beispielen ist erkennbar, dass nach wie vor Jungen abgewertet, sanktioniert und beschämt werden, anstatt gefördert oder gestärkt. In dieser männlichkeitsablehnenden Welt wachsen unsere Söhne auf. Dass Jungen im Kindergarten insbesondere im Bereich Motorik und Sprachfähigkeit Förderung bräuchten, da sie sich hier tendenziell langsamer entwickeln, scheint in der Fachwelt der Erziehungswissenschaften noch nicht angekommen zu sein. Dadurch haben Jungen zum Beginn der Schule nach wie vor die schlechteren Startchancen.
 

Die Zukunft der Jungenpolitik – endlich Jungenförderpolitik oder nur effektivere Jungenverliererpolitik?

Die Erfahrung hat gezeigt, dass die bisherigen geschlechterpolitischen Einrichtungen nicht geeignet sind, die berechtigten Anliegen und Belange von Jungen und männlichen Jugendlichen zu berücksichtigen. Die Gleichstellungsstellen (soweit es nicht immer noch reine Frauenbeauftragtenstellen sind) auf den verschiedenen politischen Ebenen zeigen entweder keinerlei ernsthaftes Interesse an dem Thema oder haben keine Zeit, um sich der längst notwendigen Jungenförderung zu widmen. Die wenigen positiven Ausnahmen bestätigen lediglich die Regel.

Die ehemalige Vizesprecherin der rot-grünen Bundesregierung unter Gerhard Schröder, Charima Reinhardt, brachte es in einer Kolumne auf FR-online[65] auf den Punkt:

„Familienministerin Ursula von der Leyen hat es bisher verstanden, sich bei Forderungen nach gezielter Jungenförderung taub zu stellen.“

Und das behauptet immerhin die Vizesprecherin der Regierung, die Jungen die Teilnahme am Zukunftstag verwehrt hat, also nicht gerade eine sehr jungenfreundliche Regierung. Ein unglücklicher Umstand ist, dass das Bundesjugendministerium und Bundesfrauenministerium unter einem Dach vereint sind. Eine Verknüpfung, die häufig auch auf Länderebene zu finden ist. Und Frauenministerinnen interessieren sich für die Frauenquote. Dass da natürlich wenig Interesse an Jungenförderung besteht, liegt auf der Hand. Dadurch werden Jungen in der geschlechtersensiblen Förderung immer das Nachsehen haben.

Auch die von Kanzlerin Merkel und der neuen Bundesjugendministerin Schröder angekündigte „Jungenförderung“ ist bei nüchterner Betrachtung der bisherigen Konzeption bislang eher enttäuschend. Die Internetpräsenz des neuen Referats „Gleichstellungspolitik für Jungen und Männer“ im Frauenministerium (!) zeigt, mit Stand vom 10.04.2010, als Schwerpunkt lediglich eine effektivere Nutzung von jungen Männern als Zivildienstleistende. Weder der Wunsch nach einer stärkeren Integration von jungen Männern in erzieherische oder pädagogische Berufe noch die Beseitigung des geschlechterspezifischen Bildungsgefälles zuungunsten der Jungen noch die problematische Situation von männlichen Jugendlichen mit Migrationshintergrund wird auch nur ansatzweise erwähnt.
Jungenförderung bedeutet nach Ansicht der Bundesregierung offensichtlich weniger, das Bildungspotenzial von Jungen und jungen Männern besser auszuschöpfen, sondern eher, das Zivildienstpotential von jungen Männern besser zu nutzen.

Was wir brauchen, ist eine eigenständige, nicht ideologische, von der Frauenpolitik unabhängige Jungen- und Männerpolitik, die geeignet ist, die legitimen Anliegen und Belange von Jungen und Männern in die geschlechterpolitische Diskussion einzubringen. Dazu benötigen wir jedoch Politikerinnen und Politiker, die die zunehmenden Bildungs- und Zukunftsmisserfolge von Jungen als das erkennen, was sie sind, nämlich eine große jugend- und bildungspolitische Herausforderung, und nicht ein Grund zum Feiern.

Wir möchten nochmals klarstellen, dass die zunehmenden Bildungs- und Zukunftsmisserfolge von Jungen den Geschlechterdiskurs keineswegs verkürzt darstellen, wie dies suggeriert wird, sondern eindeutig belegbar sind. Desweiteren sind die zunehmenden Bildungsmisserfolge von Jungen kein Zufall und schon gar nicht die Schuld der Jungen selber, sondern die logische Folge einer seit Jahrzehnten andauernden Jungenvernachlässigung und –ausgrenzung, für die die Bildungs- und Jugendpolitik, und damit auch ihre Einrichtungen, die Verantwortung tragen.

Es bleibt die Hoffnung, dass die neue Jugendministerin Dr. Schröder sich nicht primär als Frauenministerin sieht, wie ihre Vorgängerinnen, sondern als Jugendministerin mehr Verständnis für die legitimen Anliegen und Belange von Jungen aufbringen möge als es ihre Vorgängerinnen taten. Er wäre dringend erforderlich. Die bisherigen Entwicklungen sind jedoch eher ernüchternd.
 

---

[1] Aktionsrat Bildung – Vereinigung der Bayerischen Wirtschaft e. V. (Hrsg.) (2009): Geschlechterdifferenzen im Bildungssystem. Aktionsrat Bildung. Jahresgutachten 2009. Wiesbaden, S.11 [2] Autorengruppe Bildungsberichterstattung (2008): Bildung in Deutschland 2008. Ein indikatorengestützter Bericht mit einer Analyse zu Übergängen im Anschluss an den Sekundarbereich I. Bielefeld, S. 11f.
[3] Berlin-Institut für Bevölkerung und Entwicklung (Hrsg.) (2007): Not am Mann. Von Helden der Arbeit zur neuen Unterschicht? Lebenslagen junger Erwachsener in wirtschaftlichen Abstiegsregionen der neuen Bundesländer. Berlin, S. 44 ff.
[4] MANNdat-Studie „Berücksichtigung jungenspezifischer Belange in den für Bildung zuständigen Ministerien in Deutschland 2008“ S. 4f.
[5] „Bildung in Freiburg 2008, herausgegeben von der Stadt Freiburg im Breisgau, S. 58
[6] Kottmann, B. (2006): Selektion in die Sonderschule. Das Verfahren zur Feststellung von sonderpädagogischem Förderbedarf als Gegenstand empirischer Forschung. Bad Heilbrunn: Julius Klinkhardt
[7] Diefenbach, Heike (2008): Jungen und schulische Bildung. In: Matzner, M./ Tischner, W. (Hrsg.): „Handbuch Jungen-Pädagogik“. Weinheim: Beltz, S. 99.
[8] Vgl. http://de.wikipedia.org/wiki/Yasemin_Karaka%C5%9Fo%C4%9Flu Abruf 15.10.09
[9] http://www.bundesjugendkuratorium.de/bjk.html  Abruf 19.10.09
[10] Aus „Fachstelle Jungenarbeit Rheinland-Pfalz/Saarland“ Abruf 18.11.09 http://www.jungenarbeit-online.de/
print.jsp?jsessionid=C885A3DF5907DAD4E945A98146FB3BCF&kontext=Kontext_77&auswahl=65&dwgroup=null&dwview=default&printversion=true
[11] Wo bleiben die Jungs? Statusbericht über die Jungenförderung im Landkreis Karlsruhe von Dr. Bruno Köhler 2009
[12] http://www.schuelerinnen-forschen.de/uploads/media/Flyer-sch%C3%BClerinnen-forschen.pdf Abruf 21.12.09
[13] http://www.studieninfo-bw.de/servicenav/aktuelles/presse_detail/kursbuch/////2a11959a48/article/1904/805/ Abruf 21.12.09
[14] Meurer M., Haase A. „Es muss irgendwie weiter gehen“ Beitrag in switschborad Nr.190, S.48
[15] Stellungnahme Bundesjugendkuratorium S. 23
[16] Boos-Nünning, Ursula/Karakasoglu, Yasemin (2005): Viele Welten leben. Zur Lebenssituation von Mädchen und jungen Frauen mit Migrationshintergrund, Waxmann-Verlag, Münster.
[17] Nationaler Integrationsplan der Bundesregierung 2007 Themenfeld 4.4
[18] Zitat aus der Ablehnungsbegründung des BMFSFJ bezüglich unserer Petition Nr. 3-16-17-2162-006758:” Vor der Studie “Viele Welten leben” standen daher keine gesicherten Daten zur Lebenssituation von Mädchen mit Migrationshintergrund zur Verfügung. Zugleich liegen jedoch eine Reihe von Studien vor, die sich ausschließlich mit männlichen jungen Zugewanderten beschäftigen.”
[19] BMBF: „Bildungsmisserfolge von Jungen“, S. 6
[20] http://bbfk.netletter.at/mmedia/2008.07.08/1215535449.pdf Abruf 12.10.09
[21] http://de.wikipedia.org/wiki/Yasemin_Karaka%C5%9Fo%C4%9Flu Abruf 15.10.09
[22] Auszug aus dem Koalitionsvertrag von CDU/CSU/FDP vom Oktober 2009
[23] http://idw-online.de/pages/de/news334694   Abruf 12.10.09
[24] „Deutschland braucht zusätzlich 40.000 Erzieher“ http://www.spiegel.de/politik/deutschland/0,1518,679012,00.html  Abruf 15.03.2010
[25] Bischof-Köhler, Doris (2008): Geschlechtstypisches Verhalten von Jungen aus evolutionstheoretischer und entwicklungspsychologischer Perspektive. In: Matzner, M./ Tischner, W. (Hrsg.): „Handbuch Jungen-Pädagogik“. Weinheim: Beltz, S. 18-33
[26] Strüber, Daniel (2008): Geschlechtsunterschiede im Verhalten und ihre hirnbiologischen Grundlagen. In: Matzner, M./ Tischner, W. (Hrsg.): „Handbuch Jungen-Pädagogik“. Weinheim: Beltz, S. 34-48
[27] Bischof-Köhler, Doris (2008): Geschlechtstypisches Verhalten von Jungen aus evolutionstheoretischer und entwicklungspsychologischer Perspektive. In: Matzner, M./ Tischner, W. (Hrsg.): „Handbuch Jungen-Pädagogik“. Weinheim: Beltz, S. 33
[28] Hurrelmann, zitiert im Vortrag von Petra Tzschoppe in der „Vorlesungsreihe Aspekte der Soziologie in der Rehabilitation – Thema 3: Sozialisation und Gesundheit“, http://sportfak.uni-leipzig.de/~fg-sportsoziologie/documents/SozialisationundGesundheit_000.pdf Abruf 24.01.2010
[29] Guggenbühl, Allan (2008): Die Schule – ein weibliches Biotop?. In: Matzner, M./ Tischner, W. (Hrsg.): „Handbuch Jungen-Pädagogik“. Weinheim: Beltz, S. 167
[30] Tischner, Wolfgang (2008): Bildungsbenachteiligung von Jungen. In: Matzner, M./ Tischner, W. (Hrsg.): „Handbuch Jungen-Pädagogik“. Weinheim: Beltz, S. 351
[31] Kultusministerium von Baden-Württemberg – Antwort auf Antrag Abg. Andrea Krüger u.a. CDU 18.09.07 Drucksache 14/1682
[32] Jugendministerin Ursula von der Leyen (CDU), in einem Interview in der Berliner Zeitung 29.09.2006
[33] Rohrmann, Tim (2008): Jungen in der Grundschule. In: Matzner, M./ Tischner, W. (Hrsg.): „Handbuch Jungen-Pädagogik“. Weinheim: Beltz, S. 113
[34] MANNdat-Studie „Jungen und Männer in Deutschland 2007“ S. 15
[35] PISA 2006: Naturwissenschaftliche Kompetenzen für die Welt von Morgen – OECD Briefing Note für Deutschland S. 33  http://www.oecd.org/dataoecd/60/3/39727140.pdf  Abruf 12.10.09
[36] Studie vom BMFSFJ „Bildungs(miss)erfolge von Jungen…“ S. 16 und 20
[37] Aufenanger, Stefan (2008): Jungen und Medien. In: Matzner, M./ Tischner, W. (Hrsg.): „Handbuch Jungen-Pädagogik“. Weinheim: Beltz, S. 299
[38] Garbe, Christine (2008): Echte Kerle lesen nicht!? In: Matzner, M./ Tischner, W. (Hrsg.): „Handbuch Jungen-Pädagogik“. Weinheim: Beltz, S. 305
[39] Stellungnahme Bundesjugendkuratorium S.11
[40] BMBF: „Bildungsmisserfolge von Jungen“, Seiten 22, 23, 27 und 28
[41] Matzner, Michael/Tischner, Wolfgang (2008): Auf dem Weg zu einer Jungenpädagogik . In: Matzner, M./ Tischner, W. (Hrsg.): „Handbuch Jungen-Pädagogik“. Weinheim: Beltz, S. 392
[42] Neutzling, R. (2005): Besser arm dran als Arm ab. In: Rose, L./Schmauch, U. (Hrsg.): Jungen – die neuen Verlierer? Königstein/Taunus: Ulrike Helmer Verlag, S. 75
[43] Stellungnahme Bundesjugendkuratorium S. 15
[44] Berlin-Institut für Bevölkerung und Entwicklung (Hrsg.) (2007): Not am Mann. Von Helden der Arbeit zur neuen Unterschicht? Lebenslagen junger Erwachsener in wirtschaftlichen Abstiegsregionen der neuen Bundesländer. Berlin, S. 44 ff.
[45] http://www.arbeitsagentur.de/nn_169250/Dienststellen/RD-BY/Regensburg/AA/Presse/Presseinformationen/2009/Arbeitsmarktreport-01-09-20090012.html  Abruf 12.10.09
[46] Stellungnahme BJK S. 15
[47] Das Statistische Bundesamt meldet: “Zahl der Woche“ vom 31. Oktober 2006 Immer weniger Studienabschlüsse von Männern
[48] Matzner, Michael/Tischner, Wolfgang (2008): Auf dem Weg zu einer Jungenpädagogik . In: Matzner, M./ Tischner, W. (Hrsg.): „Handbuch Jungen-Pädagogik“. Weinheim: Beltz, S. 383
[49] Schultheis, Klaudia (2008): Jungenforschung. In: Matzner, M./ Tischner, W. (Hrsg.): „Handbuch Jungen-Pädagogik“. Weinheim: Beltz, S. 370
[50] nach Harmgarth 1997 aus E.Gläser, G. Franke-Zöllmer „Lesekompetenz fördern von Anfang an“, Schneider-Verlag Hohengehren, Baltmannsweiler 2005; Beitrag von C.Garbe „Lesekompetenz als Schlüsselqualifikation“ S.17f.
[51] BMBF: „Bildungsmisserfolge von Jungen“, S.6, 11, 16
[52] Matzner, Michael/Tischner, Wolfgang (2008): Auf dem Weg zu einer Jungenpädagogik . In: Matzner, M./ Tischner, W. (Hrsg.): „Handbuch Jungen-Pädagogik“. Weinheim: Beltz, S. 391
[53] Matzner, Michael/Tischner, Wolfgang (2008): Auf dem Weg zu einer Jungenpädagogik . In: Matzner, M./ Tischner, W. (Hrsg.): „Handbuch Jungen-Pädagogik“. Weinheim: Beltz, S. 392
[54] ADHS – Aufmerksamkeitsdefizit-Hyperaktivitätsstörung  http://www.neurologen-und-psychiater-im-netz.de/npin/npinkrankheit/show.php3?id=110&nodeid=21 Abruf 21.12.09
[55] „Pillen allein reichen nicht“ http://www.berlinonline.de/berliner-zeitung/archiv/.bin/dump.fcgi/2001/0926/wissenschaft/0256/index.html Abruf 21.12.09
[56] ADHS – Immer mehr Kinder in Baden-Württemberg schlucken Pillen http://www.pressemitteilungen-online.de/index.php/adhs-immer-mehr-kinder-in-baden-wuerttemberg-schlucken-pillen/ Abruf 21.12.09
[57] Stellungnahme Bundesjugendkuratorium S. 2
[58] Diefenbach, Heike (2008): Jungen und schulische Bildung. In: Matzner, M./ Tischner, W. (Hrsg.): „Handbuch Jungen-Pädagogik“. Weinheim: Beltz, S. 100f.
[59] http://www.dji.de/cgi-bin/projekte/output.php?projekt=192  Abruf 14.10.09
[60] Stellungnahme Bundesjugendkuratorium „Schlaue Mädchen – Dumme Jungen? Gegen Verkürzungen im aktuellen Geschlechterdiskurs“, September 2009, S. 14
[61] Datenbank Praktikumsdaten „Respekt Jungs“ und Datenbank „Girls-Day“ zum 10.10.09
[62] PM zum BAUA-Mobbing-Report 2008 http://www.sueddeutsche.de/jobkarriere/553/442293/text/  Abruf 18.11.09

 [63] PM zum Antierzieherurteil http://www.openpr.de/news/231281/Richter-sehen-maennliche-Erzieher-als-nicht-tragbar-an.html  Abruf 18.11.09

[64] MENSCHENKENNTNIS, Zürich, Heft 7-8/1991, Artikel „Zum gesellschafts- und wertezersetzenden Charakter des Feminismus“
[65] Charima Reinhardt in „Männerpolitik? Zum Teufel damit!“   http://www.fr-online.de/in_und_ausland/politik/meinung/2053243_Kolumne-Maennerpolitik-Zum-Teufel-damit.html&em_comment_page=3#show_comments Abruf 14.11.09