aus spektrum.de, 17. 5. 2024 zu Jochen Ebmeiers Realien
In der Geschichte der Teilchenphysik wird ein entscheidender Teil häufig ausgelas-sen. So gibt es zahlreiche Bücher zu den Anfängen der Quantenmechanik, ebenso zum heutigen Stand der Forschung, etwa der Suche nach einer Weltformel. Oft scheint es, als habe man mit der Begründung der Quantenmechanik gleichzeitig alles über die Teilchenphysik gewusst. Doch der Eindruck trügt. Tatsächlich standen Physikerinnen und Physiker in den 1950er und 1960er Jahren vor großen Rätseln. Erst abstrakte Konzepte aus der Mathematik konnten die seltsamen Beobachtungen erklären – und führten schließlich zum Standardmodell der Teilchenphysik.
Und damit nicht genug: In den folgenden Jahrzehnten entdeckten Fachleute immer mehr neue Teilchen. In so genannten Blasenkammern beobachteten sie die Spuren von bisher unbekannten Partikeln, die aus dem All auf die Erde herabregneten. Und auch die ersten Teilchenbeschleuniger lieferten Hinweise auf bisher ungeahnte Teilchen. In den 1950er Jahren hatte die Fachwelt einen ganzen Katalog mit dutzenden Einträgen gesammelt. Darin fanden sich etwa Positronen (Antiteilchen des Elektrons), Myonen (die schweren Geschwister des Elektrons), verschiedene Pionen, Kaonen, Sigma-Baryonen und so weiter. Die Liste wuchs so schnell und chaotisch an, dass Robert Oppenheimer von einem Teilchenzoo sprach.
Es war schwer, den Überblick zu behalten. Das stellte die Fachleute vor eine geradezu metaphysische Frage: Ist unser Universum wirklich so komplex? Gibt es tatsächlich eine Myriade verschiedener Grundbausteine, aus denen sich die Natur nach komplizierten Regeln zusammensetzt?
Ein Physiker schafft Ordnung
Um sich einen besseren Überblick zu verschaffen, fingen Physiker und Physikerinnen an, die Teilchen gemäß ihrer Eigenschaften zu ordnen. Zum einen ließen sich die Masse und die elektrische Ladung der Partikel aufzeichnen, ebenso wie ein quantenmechanisches Merkmal namens Spin. Letzteren kann man sich wie eine Art Minimagnet vorstellen, den Teilchen mit sich tragen und der verschiedene Ausrichtungen besitzen kann. Zum anderen erkannten die Fachleute, dass manche Teilchen ein seltsames Verhalten an den Tag legen: Kaonen und Hyperonen entstehen beispielsweise recht schnell in Teilchenbeschleunigern, zerfallen trotz ihrer hohen Masse aber erstaunlich langsam. Das schien so ungewöhnlich, dass Physiker diesen Teilchen eine Eigenschaft namens Strangeness zuordneten.
Der Physiker Murray Gell-Mann begann in den 1960er Jahren, die Teilchen anhand ihrer Eigenschaften zu gruppieren und grafisch darzustellen. Er trennte zunächst Elektronen, Myonen und Photonen von den restlichen Teilchen, da sie sich völlig anders verhielten. Dann separierte er so genannte Mesonen und Baryonen voneinander, die sich in ihrem Spin unterscheiden. Dann spaltete er die Gruppen weiter. Am Ende hatte er mehrere einzelne Grüppchen mit je acht bis zehn Teilchen. Diese verzeichnete er jeweils in einem Koordinatensystem: Die x-Achse entsprach der elektrischen Ladung der Teilchen, die y-Achse ihrer Strangeness. Dabei fand Gell-Mann eine extrem symmetrische Verteilung vor, die er als »Eightfold Way« bezeichnete (auf Deutsch der Achtfache Weg, in Anlehnung an den Achtfachen Pfad des Buddhismus zur Weisheit).
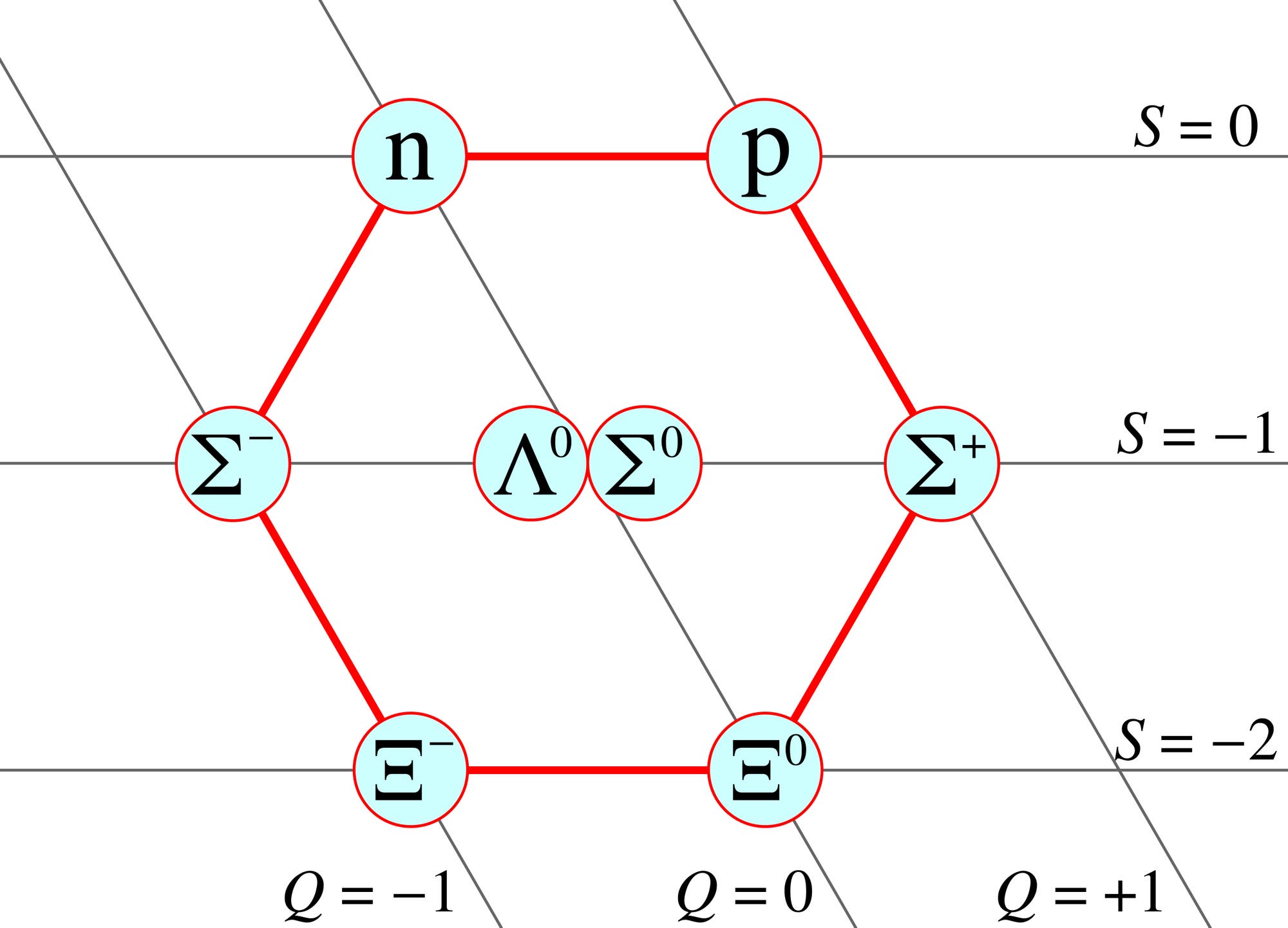Baryonen-Oktett | Trägt man
verschiedene Baryonen, zu denen auch das Neutron und das Proton gehören,
gemäß ihrer Eigenschaften auf, ordnen sich die Teilchen in einem
symmetrischen Muster ein. Einige Gruppen formen ein Sechseck, wobei zwei der Teilchen in dessen Mittelpunkt liegen. Gell-Mann fand mehrere solcher »Oktetts« vor, aber auch »Dekupletts«, bei denen sich zehn Teilchen in Form eines Dreiecks ordnen. In einem der Dekupletts schien ein Teilchen zu fehlen: Eine Stelle des Diagramms war noch unbesetzt. Gell-Mann folgerte 1962 daraus, dass dieses fehlende Teilchen existieren müsste – und wirklich wurde es zwei Jahre später in einem Teilchenbeschleuniger nachgewiesen.
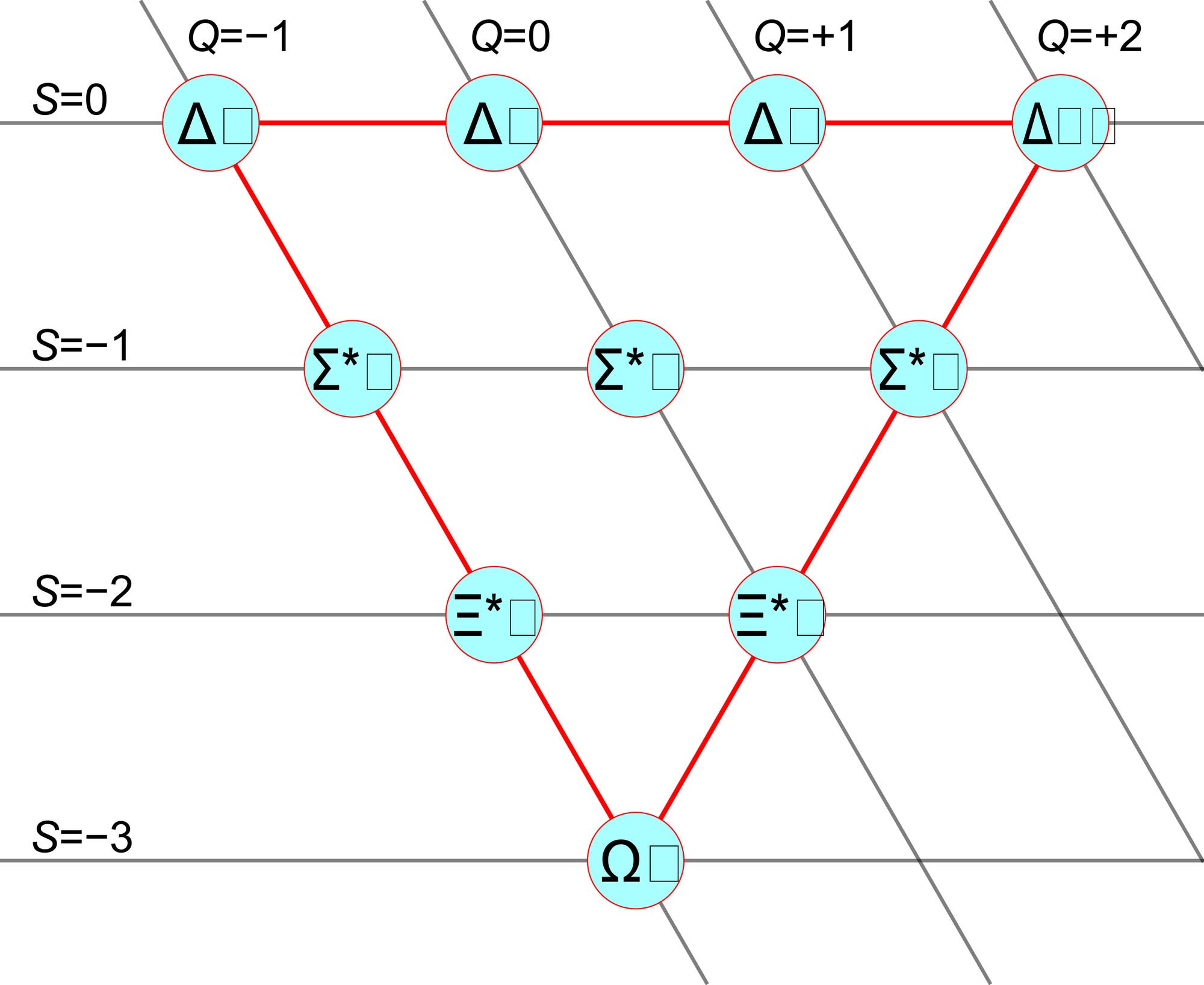Dekuplett | Die symmetrische Struktur, in die sich die
vielen verschiedenen Teilchen einordnen, legt nahe, dass sie irgendwie
miteinander verbunden sind. Als sich Gell-Mann mit Mathematikern darüber
unterhielt, erkannten sie die Muster schnell wieder. Die Oktetts und
Dekupletts entsprechen zwei Darstellungen einer bekannten
Symmetriegruppe.
Die Gruppentheorie kommt zu Hilfe
Die Gruppentheorie ist ein Teilgebiet der Algebra, das im 19. Jahrhundert entstand. Damals erkannte der gerade einmal 18-jährige Évariste Galois, dass Symmetrien nicht nur eine passive Eigenschaft einer Figur sind. Tatsächlich kann man mit Symmetrien rechnen, ähnlich wie mit gewöhnlichen Zahlen. Man kann beispielsweise Drehungen und Spiegelungen hintereinander ausführen, was der Multiplikation zweier Zahlen gleichkommt.
Gruppentheorie für Einsteiger
Am einfachsten lässt sich eine Gruppe als Menge von Symmetrietransformationen veranschaulichen. Rotiert man beispielsweise ein gleichseitiges Dreieck um 120°, ändert sich dessen Form nicht. Ein solches Dreieck kann um insgesamt drei Winkel gedreht werden (0°, 120° und 240°). Jede dieser Drehungen ist eine Symmetrietransformation. Zusammen bilden sie eine endliche Gruppe.
Neben den Drehungen kann das Dreieck auch entlang seiner Mittelachse gespiegelt werden. Die genannten Drehungen und Spiegelungen bilden jeweils für sich »Untergruppen« der gesamten Symmetriegruppe des Dreiecks.
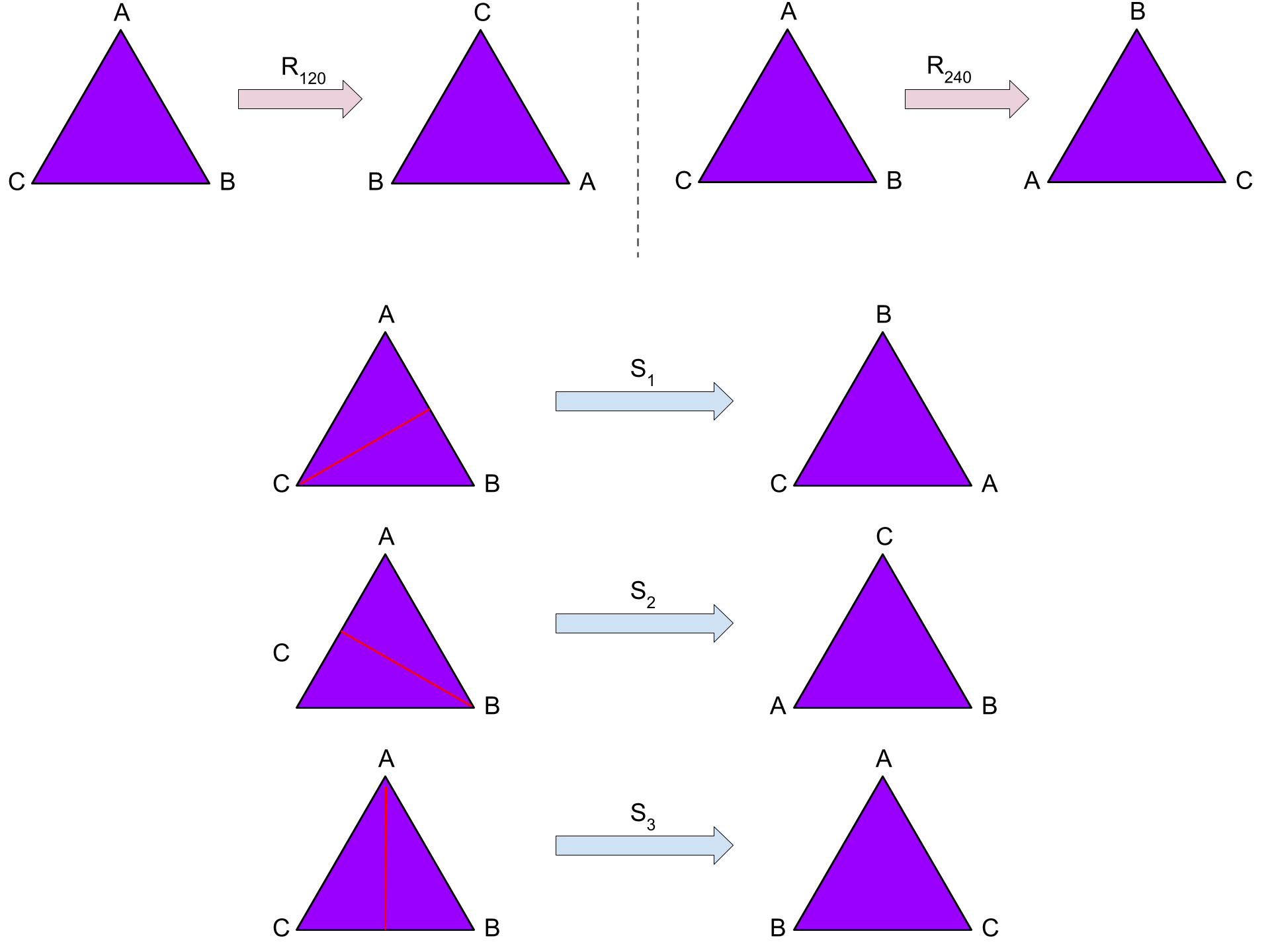
Streng genommen ist eine Gruppe aber abstrakter definiert. Sie definiert eine Menge, deren Elemente gewissen Regeln genügen: Die Verknüpfung zweier Elemente (etwa die Hintereinanderausführung zweier Drehungen) muss wieder ein Gruppenelement ergeben. Jede Gruppe enthält zudem ein »neutrales Element«, das jedes andere unverändert lässt, wie etwa die Multiplikation mit eins oder die Addition mit null. Darüber hinaus muss jedes Element auch ein Gegenstück (»inverses Element«) besitzen, so dass die Verknüpfung beider wieder das neutrale erzeugt – zum Beispiel muss man jede Drehung auch in umgekehrter Richtung ausführen können.
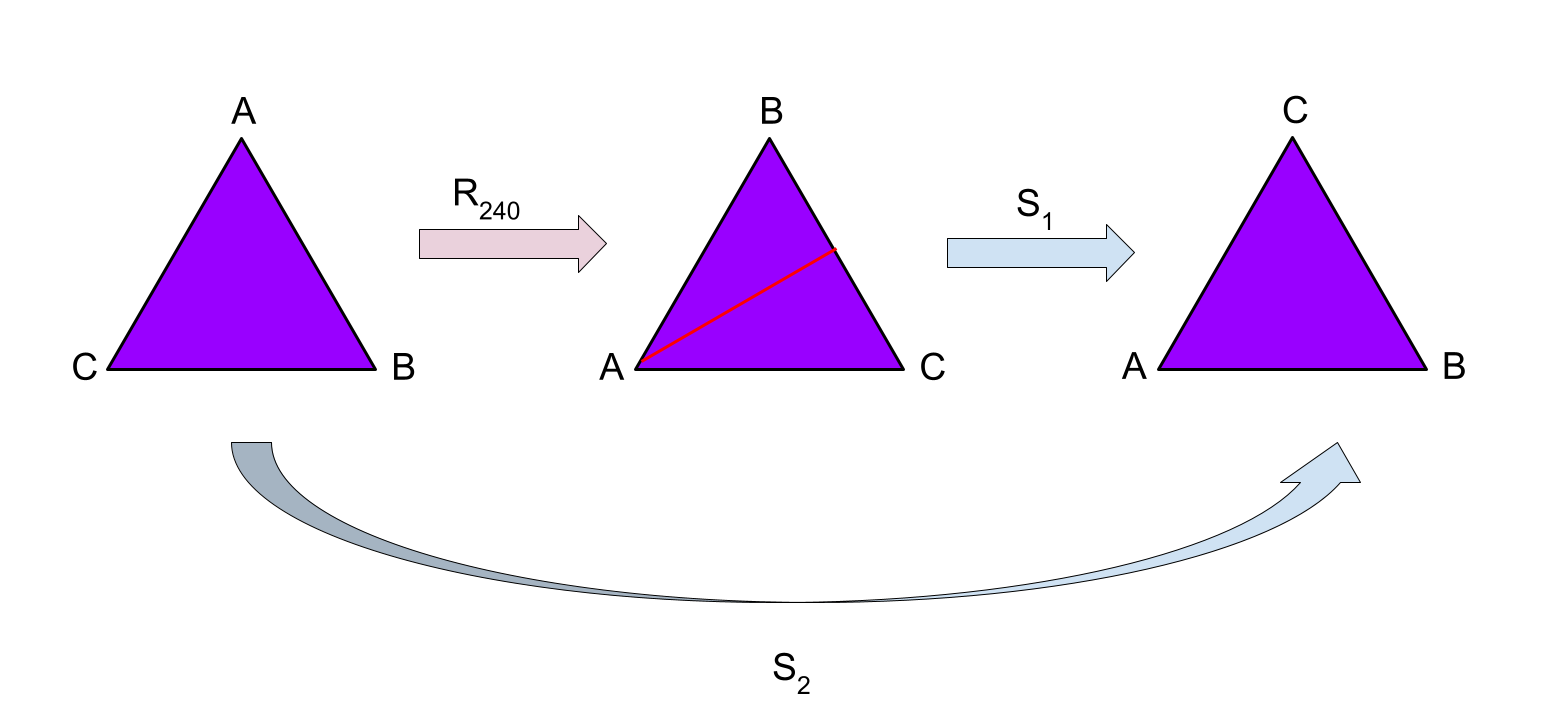
Verknüpfung von Operationen
Was genau die Elemente der Gruppe sind, spielt dabei keine Rolle. Es kann sich um Symmetrietransformationen wie Drehungen und Spiegelungen handeln, aber auch um Zahlen. So bilden etwa die rationalen Zahlen mit der Multiplikation eine Gruppe: Die Verknüpfung (das Produkt) zweier rationaler Zahlen liefert stets ein rationales Ergebnis; das neutrale Element ist die Eins und das inverse Element der Kehrwert einer Zahl.
Man kann alle Symmetrieoperationen zu einem bestimmten Objekt (etwa einer geometrischen Form) zu einer so genannten Gruppe zusammenfassen. Das hob die Mathematik und insbesondere den Bereich der Algebra auf eine abstrakte Ebene. Plötzlich ging es nicht mehr um die Objekte selbst – um geometrische Formen, Zahlen oder Gleichungen –, sondern um ihre Beziehungen untereinander.
Für Physiker, die an konkreten Ergebnissen interessiert sind, war die Gruppentheorie anfangs ein Buch mit sieben Siegeln. Viele Konzepte schienen so abstrakt, dass sie kaum offensichtliche Anwendungen hatten. Das änderte sich, als der Physiker Eugene Wigner in den 1930er Jahren und später auch Gell-Mann den enormen Nutzen der Theorie für die Physik erkannten.
Darstellungen einer Gruppe
Eine Gruppe ist zunächst eine Menge: eine Sammlung von Objekten. Doch tatsächlich besitzt jede Gruppe eine Darstellung, was sehr hilfreich ist, um die abstrakten Konzepte zu visualisieren. Die Idee dahinter: Man zeichnet einen Punkt in ein Koordinatensystem ein und wendet dann die Gruppenelemente darauf an, die den Punkt in der Ebene verschieben. Enthält eine Gruppe beispielsweise eine Spiegelung, dann wird der Punkt entsprechend an einer Achse gespiegelt. Wenn man die Bewegung des Punkts verzeichnet, ergibt sich daraus ein symmetrisches Muster, das die Wirkung der Gruppe repräsentiert.
Damit lässt sich eine Gruppe also aus mathematischer Sicht als Sammlung von Matrizen (eine Tabelle) darstellen. Allerdings stellt sich heraus: Diese Darstellung ist nicht eindeutig. Manche Gruppen kann man beispielsweise durch mehrere 3x3-Matrizen darstellen, aber auch durch 8x8-Matrizen. Beide Varianten spiegeln die Symmetrietransformationen der Gruppe wider.
Diese unterschiedlichen Darstellungen liefern für jede Gruppe charakteristische Muster. Im Fall der so genannten SU(3)-Gruppe entsprechen die Punktmuster in der einen Darstellung (mit 3x3-Matrizen) einem Oktett, in der nächstgrößeren (mit 8x8-Matrizen) einem Dekuplett – jenen Mustern, die Gell-Mann aufgezeichnet hatte. SU(3) bedeutet, anschaulich gesprochen, dass es eine Symmetrie zwischen drei verschiedenen Objekten gibt. Wenn man sich demnach ein Teilchen in Gell-Manns Oktett herauspickt und eine SU(3)-Symmetrietransformation darauf anwendet, das heißt eines der drei Objekte durch ein anderes austauscht, dann landet man zwangsläufig bei einem anderen Teilchen in dem Oktett. Die Frage war also: Was sind die drei Objekte, welche die Symmetrie erzeugen?
Zusammen mit seinem Kollegen George Zweig stellte Gell-Mann eine kühne Vermutung auf: Diese Objekte könnten noch unbekannte Elementarteilchen sein. Die beiden Physiker legten nahe, dass das Proton, das Neutron, die Kaonen und der ganze übrige Teilchenzoo gar nicht elementar sind, sondern alle aus denselben drei Grundbausteinen bestehen, den »Quarks«. Diese sollten in drei verschiedenen Sorten vorkommen und somit die beobachtete SU(3)-Symmetrie erzeugen. Bei der Namensgebung ließ sich Gell-Mann vom Roman »Finnegans Wake« von James Joyce inspirieren, in dem es heißt: »Three quarks for Muster Mark!«
Nota. - Ich trau's mich kaum zu sagen; in einem früheren Text habe ich mir eine gewagte Fromulierung durchgehen lassen:
Mathematik
ist Konstruktionslehre. Sie beschreibt in ihrem Zeichensystem, zu
welchen Kon-strukten ich gelange, wenn ich im Reich der Zahlen
(=idealiter: in der Zeit; “wie oft?”) diese und im (idealen) Raum (”wo
lang?”) jene Operation anstelle.
Warum lässt sich die Mathematik 'auf die Welt der Dinge anwenden'?
Weil ich mir die Welt der Dinge so vorstellen kann, als ob ich sie
selber konstruiert hätte; dann beschreibt die Mathema-tik in ihrem
Zeichensystem, wie ich hätte verfahren müssen, um sie so zu konstruieren. Mathe-matik
ist das allgemeine operative Schema der möglichen Handlungen in Raum
und Zeit. Logik ist das allgemeine Schema der möglichen Handlungen in
der bloßen Vorstellung.
Mathematik war nie meine Stärke. Dieses ist aber auch kein Satz aus der Mathema-tik, sondern einer über sie. Man muss nicht notwendig in ihr zuhause sein, um et-was über ihr Dasein in der realen Welt aussagen zu dürfen. Nehmen wir also an, obiger Satz träfe zu. Dann könnte es nicht überraschen, wenn Experimentieren mit Formeln der Mathematik gelegentlich Sätze ergäben, die einen Widerpart im wirkli-chen Handeln finden. Das wären Hypothesen, die man versuchen sollte. Gelegent-lich wird man Erfolg haben - wenn sie erlauben, Experimente durchzuführen, auf die sie passen.
Tautologisch? Nein, pragmatisch und spekulativ. Doch in der Mathematik selbst wäre er bedeutungslos.
*) Bedenke: Die - s. o. - wegweisende Grundform der Symmetrie stammt nicht aus der Mathematik und ihren Operationen, sondern aus der ästhetischen Anschauung.
JE
Keine Kommentare:
Kommentar veröffentlichen